1. 线性回归
从机器学习角度而言,线性回归也属于有监督学习方法,即数据使用类似类似\(a_i^T x - b_i\)的线性预测函数来建模,并且未知的模型参数(即线性函数自变量的系数)可以通过数据来估计。在统计学中,线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。线性回归认为自变量和因变量之间是线性关系,所以拟合的模型是一条广义的直线。线性回归的代价函数可以理解为争取让所有的样本点都落在直线上,即离直线的距离很近,因此,线性回归的代价函数可以写为:
\(minimize\ f_0(x)=\parallel Ax-b \parallel^2=\sum_{i=1}^{k}(a_i^T x - b_i)^2 \quad\) (1.1)
利用最小二乘法我们可以获得该代价函数的解析表达式:
\(x=(A_T A)^{-1}A_T b\) (1.2)
2. 凸优化
在凸优化——基本概念一文中,我已经对最优化和凸优化的概念做了介绍,也介绍了最小二乘问题(即目标函数是具有线性表达式平方和的形式)。对于类似(1.1)式\((a_i^T x - b_i)^2\)的优化函数,很明显是凸优化函数,但是当样本量和特征纬度过高时,最小二乘法的计算时间会成指数增长,因此,我们一般会选择梯度下降的算法对其进行求解。
3. 梯度下降原理
梯度下降方法在wiki上的解释为如果目标函数\(F(x)\)在点\(a\)处可微且有定义,那么函数\(F(x)\)在点\(a\)沿着梯度相反的方向\(-\nabla F(a)\)下降最快。其中,\(\nabla\)为梯度算子,\(\nabla = (\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \ldots, \frac{\partial}{\partial x_n})^T\)。那么,为什么要使得下降方向为梯度的反方向呢?接下来就对该理论作简要证明。
a. 导数的定义
我们之前学习过,一维函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。假设函数\(y=f(x)\)在点\(x_0\)的某个邻域内有定义,当自变量x在点\(x_0\)处取得增量\(\vartriangle x\)时,相应地函数y取得增量\(\vartriangle y = f(x_0 + \vartriangle x) - f(x_0)\),如果当\(\vartriangle x \rightarrow 0\)时,\(\vartriangle y\)与\(\vartriangle x\)之比的极限存在,则称函数在该点可导,该极限也表示函数因变量在该点附近的变化率。因此,导数的概念就是函数变化率这一概念的精确描述。
对于多元函数,函数在某点的偏导数则对应的反应了函数值沿该坐标轴方向的变化率。对于可微函数而言,不仅有关于各个自变量的偏导数,而且有沿任何方向的方向导数。方向导数较之偏导数而言,是偏导数概念的推广,指多元函数在某点沿该向量方向变动的瞬时变化率。因为,方向导数代表函数在某点沿方向向量方向变动的大小,所以对于(1.1)式而言,我们要找到目标函数在某点变化最快的方向,从而能更快的达到目标函数的极小值。而如果一个函数在某点沿任意方向的方向导数都存在,则其中必有最大的一个。因此,我们只要证明出方向导数的极值等于其梯度的范数时,即可证明出梯度下降算法的下降方向为多元函数在该点的梯度。
b. 方向导数、偏导数和方向余弦
设\(f\)是定义于\(\mathbb{R}^n\)中某区域D上的函数,点\(p_0 \in D\),点\(p\)为一动点,如果极限\(\lim\limits_{\parallel p_0 \cdot p \parallel \rightarrow 0} \frac{f(p)-f(p_0)}{\parallel \vec{p_0 \cdot p} \parallel}\)存在,则称此极限为函数f在点\(p_0\)处沿\(\vec{p_0 \cdot p}\)方向上的方向导数。对于可微函数在某点可导而言,则在某点必然存在关于各个自变量的偏导数,而且有沿任何方向的方向导数,同时,这些方向导数还可以用偏导数来表示。
为用偏导数表征方向导数,首先要介绍方向余弦的概念,设\(\ell\)是\(n\)维非零向量,\(\ell_0=\frac{\ell}{\parallel \ell \parallel}\)为与\(\ell\)方向相同的单位方向向量,若取\(0 \leqslant \alpha_i \leqslant \pi\),使得\(\ell_0 = (cos\alpha_1, \ldots, cos\alpha_n)\),其中,\(cos^2\alpha_1 + \cdots + cos^2\alpha_n=1\),则称\((cos\alpha_1, \ldots, cos\alpha_n)\)为向量\(\ell\)的方向余弦。
所以,如果函数\(f\)在点\(p_0=(x_1, \ldots, x_n)\)处可微,向量\(\vec{p_0 \cdots p}=(\vartriangle x_1, \ldots, \vartriangle x_n)\)与\(\ell\)同向,则函数在该点沿\(\ell\)方向的方向导数为:
\(\frac{\partial f}{\partial \ell}\lvert_{p_0}=\lim\limits_{\parallel \ell \parallel \rightarrow 0} \frac{f(p_0+\parallel \ell \parallel \ell_0)-f(p_0)}{\parallel \ell \parallel}=\lim\limits_{\parallel p_0 \cdot p \parallel \rightarrow 0} \frac{f(p)-f(p_0)}{\parallel \vec{p_0 \cdot p} \parallel}=\lim\limits_{\parallel p_0 \cdot p \parallel \rightarrow 0} \frac{f(p_0+\vec{p_0 \cdot p})-f(p_0)}{\parallel \vec{p_0 \cdot p} \parallel}\);
c. 微分与函数增量表示
如果函数\(y=f(x)\)在某区间内可微,意味着函数的增量\(\vartriangle y=f(x_0+\vartriangle x)-f(x_0)\)可表示为\(\vartriangle y=A \vartriangle x+o(\vartriangle x)\),其中\(A\)是不依赖于\(\vartriangle x\)的常数,\(o(\vartriangle x)\)是\(\vartriangle x\)的高阶无穷小,即当函数的自变量有一个微小的改变时,函数的变化可以分解为两个部分:一个部分是线性部分(在一维情况下,它正比于自变量的变化量);另一部分是比增量\(\vartriangle x\)更高阶的无穷小,也就是说除以\(\vartriangle x\)后仍然会趋于零。微分的几何意义就是可以在函数的微小局部可以用直线去近似代替曲线部分,用切线段来代替曲线段。
因此,由于多元函数\(f\)可微,则函数\(f(p)-f(p_0)\)可以增量表示为:
\(f(p_0+\vec{p_0 \cdot p})-f(p_0)=f(p_0 + \vartriangle x) - f(p_0)=f(x_1 + \vartriangle x_1, \ldots, x_n + \vartriangle x_n) - f(x_1, \ldots, x_n)=\frac{\partial f}{\partial x_1}\lvert_{p_0} \vartriangle x_1 + \cdots + \frac{\partial f}{\partial x_n}\lvert_{p_0} \vartriangle x_n + o(\parallel \vec{p_0 p} \parallel)\);
d. 方向导数与梯度
因此,\(\lim\limits_{\parallel p_0 \cdot p \parallel \rightarrow 0} \frac{f(p)-f(p_0)}{\parallel \vec{p_0 \cdot p} \parallel}=\lim\limits_{\parallel p_0 \cdot p \parallel \rightarrow 0} \lbrack \frac{\partial f}{\partial x_1}\lvert_{p_0} \frac{\vartriangle x_1}{\parallel \vec{p_0 \cdot p} \parallel} + \cdots + \frac{\partial f}{\partial x_n}\lvert_{p_0} \frac{\vartriangle x_n}{\parallel \vec{p_0 \cdot p} \parallel} + \frac{o(\parallel \vec{p_0 \cdot p} \parallel)}{\parallel \vec{p_0 \cdot p} \parallel} \rbrack=\frac{\partial f}{\partial x_1}\lvert_{p_0} cos\alpha_1 + \cdots + \frac{\partial f}{\partial x_n}\lvert_{p_0} cos\alpha_n\);
上式又可以转变为\(\nabla f \cdot \ell_0=\parallel \nabla f \parallel_2 \cdot \parallel \ell_0 \parallel_2 \cdot cos(\nabla f, \ell_0)=\parallel \nabla f \parallel_2 \cdot cos(\nabla f, \ell_0)\)。
e. “多元函数沿其负梯度方向下降最快”的证明
综上所述,函数\(f\)在点\(p_0\)的方向导数\(\frac{\partial f}{\partial \ell}\lvert_{p_0}=\parallel \nabla f \parallel_2 \cdot cos(\nabla f, \ell_0)\),推导完成后,可能看到这又忘记我们要证明什么了。。。我们的目标是找到方向导数中的极值,因此,当且仅当\(cos(\nabla f, \ell_0)=1或-1\)时,可取得极值,考虑到我们是要使得目标函数最小,所以这里应该选择cos值为-1,这样目标函数会沿该方向下降最快;同理,若要使得目标函数上升最快,则应选择cos值为+1,这样目标函数会沿该方向上升最快。而cos值等于-1等价于向量\(\nabla f\)与向量\(\ell_0\)平行且方向相反,即方向导数\(\ell_0\)为梯度的负方向,此时,函数\(f\)下降最快。即证多元函数沿其负梯度方向下降最快。
3. 梯度下降算法实现过程
讲到梯度下降算法的实现,我想这里就不在特别详细介绍了,因为Andrew Ng的Coursera课程已经介绍的足够详细了,而且有matlab的代码的实现,绝大多数机器学习爱好者也学习过该课程。说到这里,不得不吐槽的是国内和国外的研究生教育方式,貌似国内的研究生乃至博士课程显得过于鸡肋,无论从学生角度还是从教师角度,课程的学习都趋向于走形式,学生眼里的我能过就行和导师万年不变的PPT都使得课程的知识传递显得苍白无力,很难像国外的教学体制中的教学一体化,所以很多中国学生在留学期间由于根基不好会非常的忙碌,这与国内教育不注重基本,流于形式有很大的关系,因为即使是国内的研究生,上课期间也很少有coding的任务。就拿Coursera上学过的课程和我在北理工学过的课程相对比,在Coursera上的计算机相关课程都会有很多coding的Assignments,而在北理工学习期间,我只上过一门图像处理的课程需要coding,而且也就是图像旋转,加一些噪声等,其他基本上就是到万方上下些论文,拼拼凑凑交个大作业的论文,及其没有营养。真的希望以后国内教学体制可以引入一些国内外好的在线课程,这样既能算学分,也可以学到知识,老师也省去些事情,两全其美~
回到线性回归和梯度下降算法,针对线性回归的代价函数\(J(\theta_0,\theta_1,\ldots,\theta_n)=\sum_{i=1}^{m}(\theta^T \cdot x^{(i)} - y^{(i)})^2\),我们可以计算出代价函数的梯度,为:\(\frac{\partial}{\partial \theta_j}J(\theta)\)。因此,梯度下降算法每次更新的\(\theta\)为\(\theta_j:= \theta_j-\alpha \frac{\partial}{\partial \theta_j}J(\theta)=\theta_j-\alpha \frac{1}{m} \sum^{m}_{i=1} (\theta x^{(i)} - y^{(i)})x^{(i)}_j\),其中,\(\theta_0\)为线性方程的截距,此时,对应的\(x^{(i)}_j=1\)。
梯度下降算法在每次迭代过程中需要注意两点:
-
每次更新向量\(\theta\)时,要用现有\(\theta\)值减去函数的梯度,因为函数沿其负梯度方向下降最快;
-
在每次迭代更新向量\(\theta\)时,要同时更新每一个\(\theta_j\),不能再一次迭代中更新完\(\theta_j\)后再更新\(\theta_{j+1}\);
4. 梯度下降算法实例
本实例采用R语言,应用iris数据中花萼的长度(Sepal.Length)来预测花瓣的长度(Petal.Length),其中\(x\)为自变量,\(y\)为因变量。具体实例代码如下,实验分别采用梯度下降算法、最小二乘法、Nelder-Mead算法和L-BFGS-B优化算法对比估计的结果:
#读取数据x和y
x <- matrix(iris[which(iris$Species != "setosa"), ]$Sepal.Length, ncol=1)
y <- matrix(iris[which(iris$Species != "setosa"), ]$Petal.Length, ncol=1)
#绘制二维数据的散点图
plot(x, y,
main="versicolor和virginica花的散点图",
sub="花萼的长度和花瓣的长度",
col="blue",
family='STKaiti' #mac下需要增加该命令,否则不显示中文字符
)
#解决mac下乱码问题可参考http://www.klshu.com/1807.html
#梯度下降算法
##1. 计算代价函数
computeCost <- function(independent, dependent, variable){
m = length(dependent)
J = 0
J = 1/(2*m)*sum((independent%*%variable-y)^2)
return (J)
}
##2. 计算梯度
gradient <- function(independent, dependent, variable, alpha, num_iters){
m = length(dependent)
n = length(variable[,1])
J_history = rep(0, num_iters)
T_history = matrix(0, nrow = num_iters, ncol = n)
for (i in 1:num_iters){
variable = variable - alpha / m * (t(x) %*% (independent %*% variable - y))
J_history[i] = computeCost(independent, dependent, variable)
T_history[i,] = variable
}
result <- list(variable, J_history, T_history)
return (result)
}
##3. 训练LR模型
xLength <- length(x[,1])
intercept <- matrix(rep(1, xLength), ncol=1)
x <- cbind(intercept, x)
theta <- matrix(rep(0, 2), ncol=1)
num_iters <- 1000
alpha <- 0.01
gradient.result <- gradient(x, y, theta, alpha, num_iters)
abline(gradient.result[[1]][1], gradient.result[[1]][2])
## 4. 最小二乘法
theta.LeastSquare <- solve(t(x) %*% x) %*% t(x) %*% y
abline(theta.LeastSquare[1], theta.LeastSquare[2],col="red")
##5. R中optim函数的默认优化算法求解
nm.optim <- optim(par = theta,fn = function(p) {computeCost(x, y, p)},
method = "Nelder-Mead", #或者采用SANN方法
control = list(trace = FALSE, maxit = 100))
abline(nm.optim$par[1], nm.optim$par[2],col="yellow")
##6. R中L-BFGS-B算法求解
gr.optim <- function(independent, dependent, variable, alpha){
m = length(dependent)
variable = alpha / m * (t(x) %*% (independent %*% variable - y))
return (variable)
}
bfgs.optim <- optim(par = theta,fn = function(p) {computeCost(x, y, p)},
gr = function(p) {gr.optim(x, y, p, alpha)},
method = "L-BFGS-B", #L-BFGS-B
control = list(trace = FALSE, maxit = 100))
abline(bfgs.optim$par[1], bfgs.optim$par[2],col="green")
#7. 输出结果
print(sprintf("初始代价函数的值为:%g",computeCost(x, y, theta)))
print(sprintf("梯度下降算法求的theta值为:%g和%g",
gradient.result[[1]][1],
gradient.result[[1]][2]))
print(sprintf("最小二乘法求的theta值为:%g和%g",
theta.LeastSquare[1],
theta.LeastSquare[2]))
print(sprintf("Nelder-Mead优化算法求的theta值为:%g和%g",
nm.optim$par[1],
nm.optim$par[2]))
print(sprintf("L-BFGS-B优化算法求的theta值为:%g和%g",
bfgs.optim$par[1],
bfgs.optim$par[2]))
legend("topleft", legend=c("gradient-descent","least square","Nelder-Mead", "L-BFGS-B"),
bty='n', col=c("black","red", "yellow", "green"),
lty = c(1, 1, 1, 1), cex=0.8, y.intersp=0.8)
#7. 学习曲线绘制
iter <- 1:50
cost <- gradient.result[[2]][1:50]
plot(iter, cost,
main="梯度下降算法学习曲线",
sub="迭代次数为1:50",
family='STKaiti')

从输出结果可以看出,四种优化算法求得的梯度和最终的代价函数的值基本一致,除了本实例实现的梯度下降算法,其余三种方法分别为单纯形算法(Nelder-Mead)、最小二乘法(Least Square)以及拟牛顿法(L-BFGS-B),当然,R中的optim函数还提供模拟退火算法(SANN)用于求解。
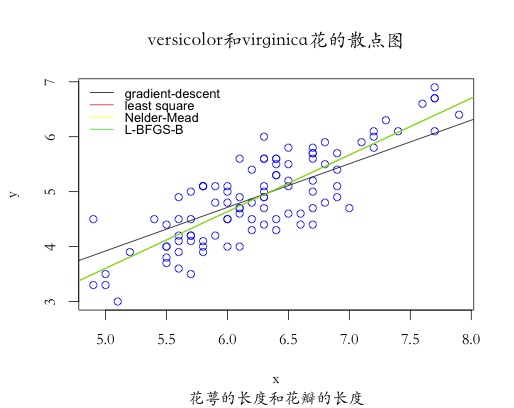
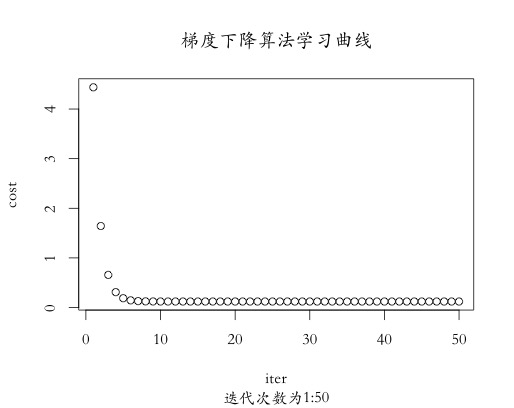
从散点图可以看出,采用梯度下降算法求解的最终结果与其他三种算法稍有偏差,是因为迭代次数少的原因,当迭代次数增加,其结果会逐渐逼近其他三种算法,从另一角度也可以证明出,原始梯度下降算法的效率并没有其他几种算法效率高,其他三种算法基本在50次以内就会达到最优值。从学习曲线结果可以看出,代价函数值呈递减趋势,符合梯度下降算法的基本特性,总体而言,传统梯度下降算法一般不用于算法的优化求解,我们经常采用改进的梯度下降优化算法来求解目标函数的极值。