{ % include JB/setup %}
注明:对于机器学习初学者而言,本篇博客里的内容实际不易于理解,如果不想过多深入研究凸优化理论的童鞋可以忽略本节内容。并且,我自己对于这部分内容理解的也不是很好,所以也许会存在不对的地方,还请看过的童鞋指正。
仿射集和凸集
a. 直线和线段
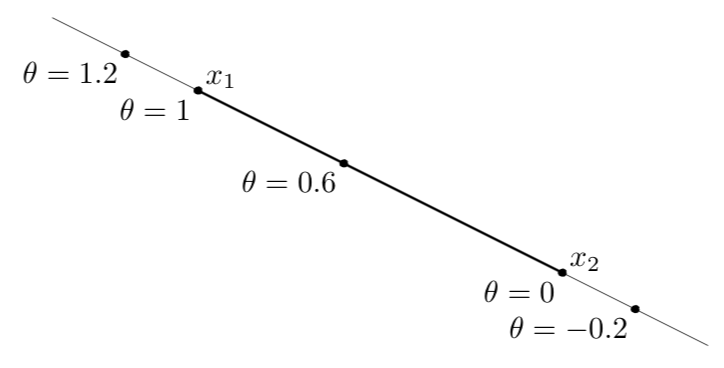
假设存在\(\mathbb\{ R\}^n\)实数空间内的不同的两点\(x_1\)和\(x_2\),那么可以构成穿越两点的直线\(y=\theta x_1 + (1-\theta)x_2\),其中,\(\theta \in \mathbb\{ R\}\)。这里\(x_1\)和\(x_2\)都是n维空间中的点,如果在指定原点的情况下,我们用向量表示他们的坐标,他那么们就代表一个n维向量。上式表示出的新点\(y\)就是通过\(x_1\)和\(x_2\)这两个点的直线上的某一点。当\(x \in \mathbb\{ R\}\)且\(\theta=0\)时,\(y\)为点\(x_2\)。同理,当\(\theta=1\)时,\(y\)为点\(x_1\)。如果\(\theta \in \{ 0,1\}\)之间内的任意值,则\(y\)可构成点\(x_1\)和\(x_2\)之间的线段,如果\(\theta \in \mathbb\{ R\}\)内任意值,则\(y\)可构成直线。如下图所示,加粗的部分表示线段,空间内整个无限长度的为直线:
b. 仿射集
对于一个集合\(C\subseteq \mathbb\{ R\}^n\),如果集合内的任意两点构成的直线仍在集合\(C\)内,则称集合\(C\)为仿射集(affine set)。换句话说,仿射集\(C\)包含该集合内任意两点的线性组合,即包含了所有经过该集合集中任意两点的直线的集合。一维空间的仿射集与我们之前提到直线的概念类似,但仿射集是一个更广意义的直线,当\(\theta\)取任意实数时,这条直线不仅在无限的空间中延展,而且没有制定空间原点的位置。
对于线性方程或线性方程组而言,如果存在方程或方程组的解,则记为集合\(C=\{ x\mid Ax=b\}\),其中,\(A \in \mathbb\{ R\}^\{ m\times n\},\ b \in \mathbb\{ R\}^m\)。此时,集合\(C\)为仿射集。因为,对于任意两个点\(x_1,\ x_2 \in C\),都会满足\(Ax_1=b,\ Ax_2=b\),对于任意\(\theta\),点\(x_1\)和\(x_2\)的线性组合仍为方程组的解。所以满足仿射集的定义(任意两点的线性组合仍在该集合内),线性方程组解的集合就是仿射集。同理,假使我们知道线性方程解的集合为仿射集,我们可以推出任意解的线性组合仍为方程的解。因此,每一个仿射集也可以表示成一系列线性方程组的解的集合的形式。
\[A(\theta x_1+ (1-\theta)x_2) = \theta Ax_1\ +\ (1-\theta)Ax_2\ = \theta b\ +\ (1-\theta)b\ =\ b\]如果集合\(C\)为仿射集,那么集合中的点\(x_1,\ldots,x_k \in C\),则\(\theta_1 x_1\ +\ \ldots\ +\ \theta_k x_k\\)称为仿射集的仿射组合(affine combination),其中,\(\theta_1\ +\ \ldots\ +\ \theta_k=1\)。很明显,仿射集中某些点的仿射组合形成的点也在该仿射集内部。仿射组合的定义有些类似线性空间的向量的线性组合。
对于任意一个集合\(C\subseteq \mathbb\{ R\}^n\),集合间所有点的仿射组合称为集合\(C\)的仿射包(affine hull),仿射包是包含某些点构成的集合\(C\)的最小仿射集。如果任意仿射集\(S\)包含集合\(C\),则集合\(C\)的仿射包是集合\(S\)的子集。我们一般将仿射包记为:
\[aff\ C\ =\ \{ \theta_1 x_1\ +\ \ldots\ +\ \theta_k x_k\ \mid\ x_1,\ldots, x_k \in C,\ \theta_1\ +\ \ldots\ +\ \theta_k=1\}\]c. 凸集
与直线和线段间的定义类似,凸集合仿射集的定义也比较相像,对于一个集合\(C\subseteq \mathbb\{ R\}^n\),如果集合内的任意两点构成的线段仍在集合\(C\)内,则称集合\(C\)为凸集。可记为:
\(\theta x_1\ + (1-\theta)x_2) \in\ C\),其中,\(0 \le \theta \le 1,\ x_1,\ x_2 \in C\)
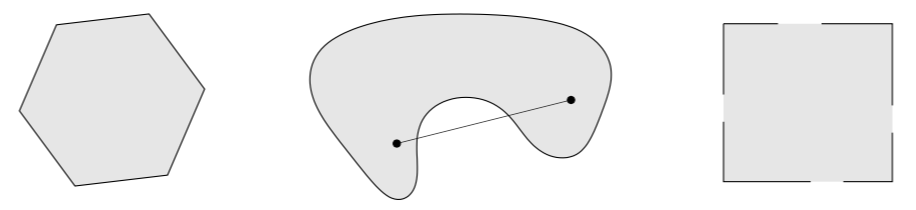
从定义我们可以看出,仿射集和凸集间的区别就在于凸集是线段在集合中。直观上理解,凸集是指集合中所有的点都可以被其他点观测到,即二者的连线仍在集合内。所以,仿射集也是凸集,因为,仿射集包含通过集合内任意两点的直线,也必然包含两点间的线段。根据凸集的定义,从下图可以看出,明显左边第一个图表示的集合为凸集,其余两个不是凸集,因为存在两点间的连线不在集合内的情况。
根据仿射集的定义,我们可以定义凸集组合(convex combination:不知道中文翻译的对不对。。。难道叫凸组合??)为:
\(\theta_1 x_1\ +\ \ldots\ +\ \theta_k x_k\\),其中,\(\theta_1\ +\ \ldots\ +\ \theta_k=1\)且\(\theta_i \ge 0\)。
应当注意的是,仿射组合和凸集组合的区别在于\(\theta\)的取值,凸集组合,中文名总觉得怪怪的。。。,在满足仿射组合定义的前提下,要求\(\theta_i \ge 0\)。
因此,对应的凸包(convex hull)则可记为:
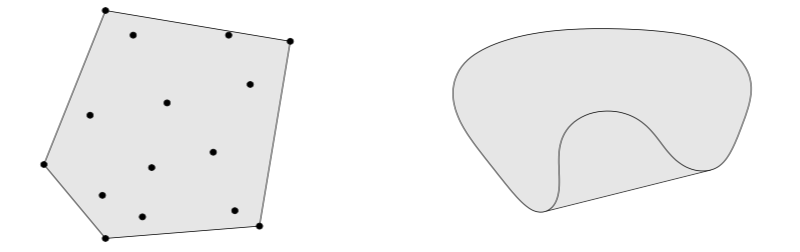
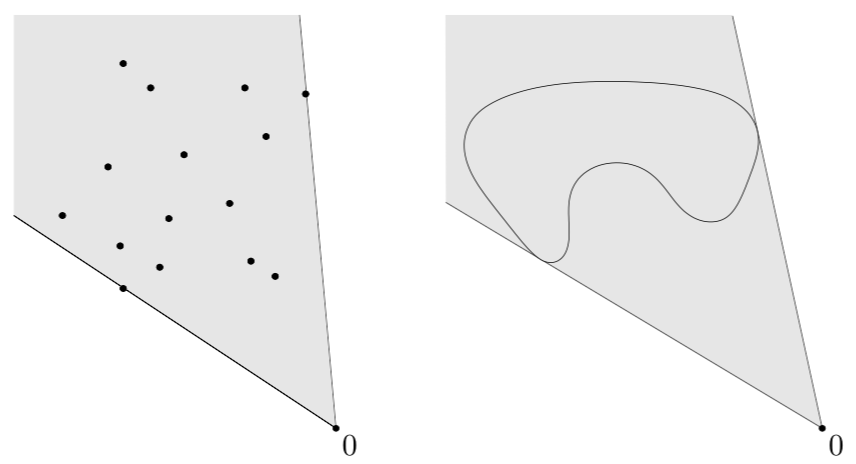
\[conv\ C\ =\ \{ \theta_1 x_1\ +\ \ldots\ +\ \theta_k x_k\ \mid\ x_1,\ldots, x_k \in C,\ \theta_1\ +\ \ldots\ +\ \theta_k=1,\ \theta_i \ge 0,\ i=1,\ldots,k\}\]从定义上来看,凸包肯定是凸集,它是包含集合C的最小凸集。从下图我们可以看出,左边第一个图中的15个点的凸包为阴影包括的多边形,第二个图中肾型集合的凸包为直线封闭下的集合。
d. 锥
锥体(cone)的定义为如果集合\(C\)中的任意点\(x\),\(\theta x \in C\),其中,\(\theta \ge 0\),则集合C称为锥。如果集合既是凸集又是锥体,我们就称该集合为凸锥(convex cone)。凸锥的数学表达为:
\(\theta x_1+\theta x_2 \in C\),其中\(x_1,\ x_2 \in C\)且\(\theta_1,\ \theta_2 \ge 0\)
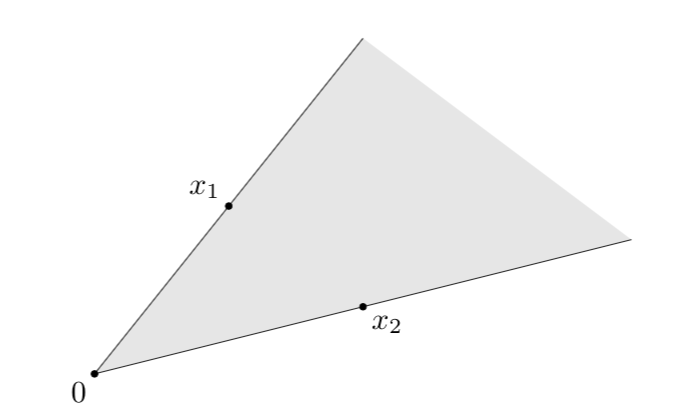
直观上看,上式定义下的凸锥为顶点为原点,以\(x_1\)和\(x_2\)为边的扇形区。如下图所示,阴影部分表示点\(x_1和x_2\)构成的凸锥,顶点对应\(\theta_1=\theta_2=0\):
凸锥中各点的线性组合我们称之为凸锥组合(conic combination),某集合\(C\)的各点的凸锥组合构成集合\(C\)的锥包(conic hull),记为:
\[\{ \theta_1 x_1\ +\ \ldots\ +\ \theta_k x_k\ \mid\ x_i \in C,\ \theta_i \ge 0,\ i=1,\ldots,k\}\]与仿射包和凸包类似,锥包也是包含集合C的最小凸锥集合。以下是两个锥包的实例,阴影部分表示集合构成的锥包,当然,顶点位置不同,所表示出的锥包也各不相同:
e. 总结
-
空集、单点和实数域的点集是仿射集,因此,也是凸集。
-
一条直线是仿射集,如果直线过原点,那么它还是凸锥。
-
一条线段是c凸集的,但不是仿射集,除非该线段仅含有一个点。
-
一条射线\(\{ x_0+\theta v \mid \theta \ge 0\}\)是凸集的,但不是仿射集,如果\(x_0\)为0, 则是凸锥。
f. 超平面和半空间
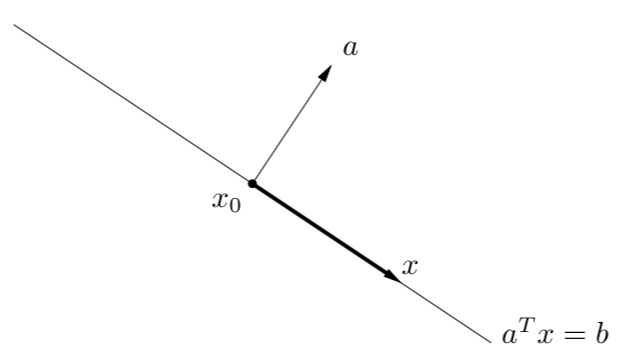
超平面(hyperplane)是\(\{ x \mid a^T x = b\}\),其中,\(a \in \mathbb\{ R\}^n,\ a \neq 0,\ b \in \mathbb\{ R\}\),该定义很简单,根据仿射集中讲到的线性方程解的例子,我们可以发现,超平面就是线性方程解的结合,如果点\(x_0\)为超平面上的点,则超平面的定义可以表示成\(\{ x \mid a^T (x-x_0) = 0\}=x_0+a^\{ \perp\}\),其中,\(a^\{ \perp\}\)表示向量\(a\)的正交分量,即垂直于向量\(a\)的点的集合,可以理解为偏移量\(x_0\)和向量a的正交分量的和。超平面是仿射集也是凸集,我们可以通过调整b的值调整超平面距离原点的距离,调整a的值来调整超平面的方向,超平面的实例如下图所示,对任意点\(x\),\(x-x_0\)(可看成是\(a^\{ \perp\}\))与向量\(a\)正交:
超平面可以将空间分为两个半空间,我们定义闭合的半空间(halfspace)为\(\{ x \mid a^T x \le b\}\),其中\(a \neq 0\)。半空间\(x \mid a^T x \ge b\)表示的是方向为\(a\)的所有的点,而半空间定义为\(\{ x \mid a^T x \le b\}\),其是方向为\(-a\)上的点的集合。因为,半空间任意点的线段在半空间内,而任意连线的直线不在半空间内(参考射线是凸集但不是仿射集),所以,半空间是凸集,但不是仿射集。如下图所示:
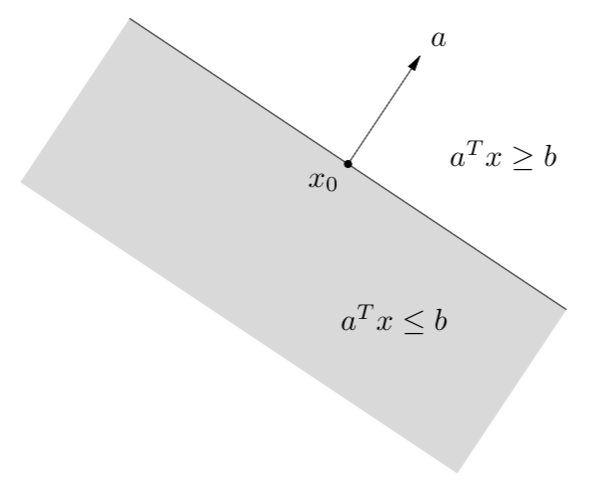
因为半空间的定义为\(\{ x \mid a^T x \le b\}\),所以根据上图我们可以发现,半空间是任何与向量\(a\)呈钝角的向量的集合。多个半平面围成的集合就称为多面体(polyhedra),关于多面体和单纯形的定义和相关概念这里就不在赘述,有兴趣的同学可以参考stanford大学Boyd教授《convex optimization》一书中的2.2.2~2.2.5节。
g. 不改变凸性的运算
不改变凸集性质的运算对于凸集而言很重要,因为凸集的优良性质会使得优化求解过程更为简单,同时,我们也可以根据具体问题构建凸函数解决对应问题。不改变凸集的运算主要有以下几种:
-
交集(intersection):如果\(S_1\)和\(S_2\)是凸集,那么\(S_1 \cap S_2\)仍为凸集。子空间、仿射集、凸锥、多面体都可以通过半空间或者超平面(二者都是凸集)构成,且每一个闭合的凸集都可以由有限个半空间的交集构成。即如果\(S_{\alpha}\)是凸集,那么\(\cap_{\alpha \in \mathbb{A}} S_{\alpha}\)仍为凸集;
-
仿射函数(affine function):在仿射集的定义中,我们提到仿射集可以被线性方程所表示,因此,具有\(f(x)=Ax\ +\ b\)形式,其中,\(A \in \mathbb\{ R\}^\{ m\times n\},\ b \in \mathbb\{ R\}^m\)的函数都可以成为仿射函数\(f:\mathbb{R}^n \rightarrow \mathbb{R}^m\)。我们先从简单的变化看起,如果\(S\subseteq \mathbb{R}^n\)是凸集,同时,\(\alpha \in \mathbb{R}\)以及\(a \in \mathbb{R}^n\),很明显,\(\alpha S=\{ \alpha x \mid x\in S \},\ S+a=\{ x+a \mid x \in S \}\)都为凸集,这两种操作称为变换(scaling)和平移(translation)。所以根据仿射函数的定义,仿射函数的变换形式仍保持原始凸集集合的性质,例如对凸集执行投影、集合相加等的操作后的集合仍为凸集。
-
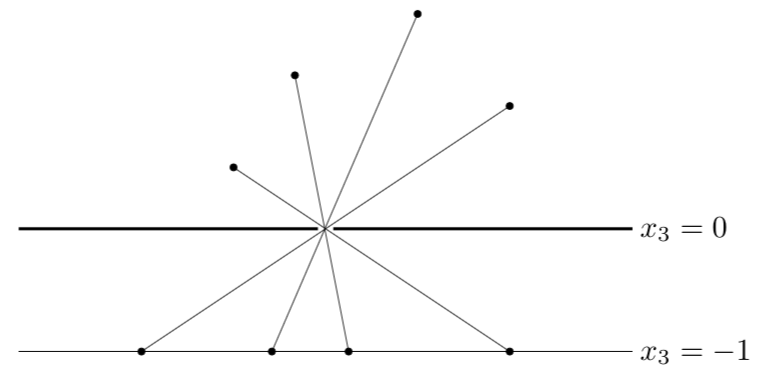
透视函数(perspective function):透视函数定义为\(P:\ \mathbb{R}^{n+1} \rightarrow \mathbb{R}^n\),透视函数通过规约变换或者归一化向量的最后一个分量,去除向量的一个维度,从n+1维降低到n维。该思想可以用初中物理学到的针孔呈像来解释。假设存在一个针孔摄像机在背面存在一个平面\(x_3=0\),一个物体\(x\in \mathbb{R}^3\)通过小孔成像映射到平面上,会使得呈像变成二维画面。如下图所示,空间上二维的点投影到一维直线\(x_3-= -1\)上,二维点的最后一个分量变成-1,成像成直线上的一个线段。很明显,如果成像前的物体为凸集,则映射后仍为凸集:
- 线性分式(linear-fractional function):定义为\(f(x)=(Ax+b) / (c^Tx+d)\),从定义可以看出,仿射函数和线性函数都是线性分式的特殊形式,这部分内容理解的还不是特别清楚,所以暂时先不写这部分的内容了。
总结
总的来说,这一节所讲述的问题比较枯燥,但是对于日后理解svm等算法会有很大帮助。具体细节等到svm篇章再做具体介绍。