题外话,来到CMU已经两周了,从刚开始的难以开口到现在可以沟通,从四处借东西蹭吃喝到现在学习做饭健身三不误,渐渐的开始适应了美国气息的生活。总的感觉,在这里无论是国人还是老外,自主性都很强,每天都有为之努力的目标,不知道这是不是跟due或者所谓的压力有关。这学期旁听了三门课,接下来要写的《凸优化》系列学习笔记就是其中之一,另两门是“16720-Computer Vision”和“10715-Advanced Introduction of Machine Learning”。在日后的时间里,我也会把机器学习相关的算法继续补充完整。
整体来说,从听课和做作业的角度来讲,CMU课程的强度之大是公认的,一学期最多修3-4门课就不错了,不像国内的课程,很多硕士一学期会选9-10门课程,然并卵,走形式而已,真正可以学到的知识少之又少。这一现象基本上是国内各大院校的普遍现象,如果想要提高国内科研水平,提高课程质量和效果是必须的。因为,CMU本科生或者硕士生一年课程代码量基本在5万行,而且对于领域相关知识的掌握很充分,相比之下,国内本科生基本不写代码,硕士毕业下来代码量也不会超过2万行,加上上课基本没什么用,所以理论与实践上的差距就体现出来了。当然,开篇废话这么多,无外乎是想把自己感受到的表达出来,生活是需要积极向上的,不能沉醉于平稳和安逸,每来到一个新的环境,总发现自己low到极点,算是学渣了吧,希望离开的时候起码可以称为合格的一员。
好了,废话不多说,开始整理凸优化课程的学习笔记,笔记可能并不会记全所有老师讲述的内容,但会把大部分我认为重要的东西保留下来~~
1. Tibshirani
感谢Ryan Tibshirani老师为这门课开源做出的贡献,希望更多人可以更好的了解凸优化,明白其在机器学习研究领域的重要性。所有课件和视频都可以在课程官网上找到。
2. 优化理论
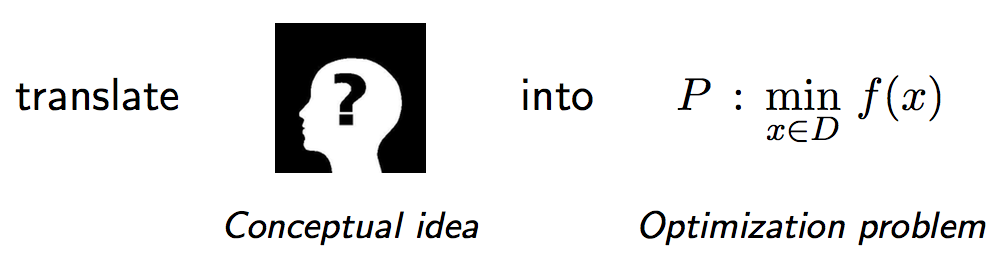
对于优化理论的定义,Ryan教授给出了一副很好理解优化理论是做什么的图,优化理论就是用于求解某个函数的极值,至于极值体现的含义就跟你要解决的问题相关了,与机器学习的“没有天生优越的分类器”的理论类似,优化算法也没有好坏之分,只有适合还是不适合解决某一问题。
3. 凸集和凸锥
a. 凸集
仿射集和凸集的概念在凸优化-凸集一文中做了详细介绍。
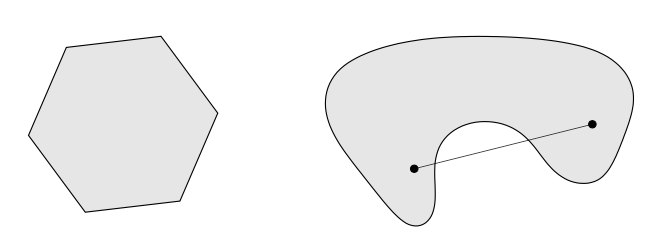
凸集为 \(C \subseteq \mathbb{R}^n\),使得\(x,y \in C \rightarrow tx+(1-t)y \in C\),其中\(0 \leq t \leq 1\)。具体表现为下图,左边第一个为凸集,第二个则不是凸集。
任何凸集的线性组合仍为凸集,所有凸集的集合为Convex hull。空集、点、线、球体(Norm ball:\(\{x: \parallel x \parallel \leq r\}\))、超平面(Hyperplane:\(\{x: a^Tx=b\}\))、半空间(Halfspace:\(\{x: a^Tx \leq b\}\))、仿射空间(Affine space:\(\{x: Ax=b \}\))和多面体(Polyhedron\(\{x: Ax \leq b \}\))均为凸集。
下面证明为什么Norm ball是凸集:
对于Norm ball中的任意两点\(x和y\),可以根据三角不等式获得:
\[\parallel tx + (1-t)y \parallel leq t \parallel x \parallel + (1-t) \parallel y \parallel \leq tr + (1-t)r \leq r\]所以,Norm ball中的任意两点\(x和y\)的线性组合仍在集合内,证明Norm ball为凸集。
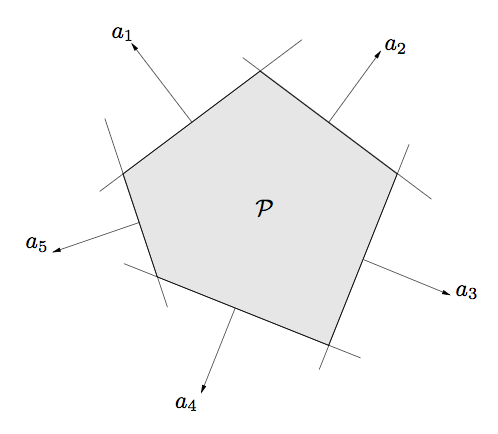
其中,Ryan还提到一个问题就是关于多面体,集合\(\{x: Ax \leq b, Cx=d\}\)是否仍是Polyhedron?
结果是显然的,仍然是多面体,因为平面\(Cx=d\)可以写成\(Cx \leq d和-Cx \leq -d\),满足Polyhedron的定义,即\(\{x: Ax \leq b\}\)。
b. 凸锥
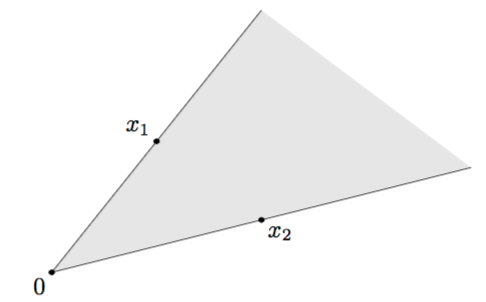
锥(cone)是指\(x \in C \rightarrow tx \in C\),其中\(t \geq 0\),而凸锥(convex cone)的定义则是\(x_1,x_2 \in C \rightarrow t_1x_1 + t_2x_2 \in C\),其中\(t_1,t_2 \geq 0\),凸锥的实例如下图:
但是,是否可以举一个例子,使得集合\(C\)为锥,但不是凸锥呢?如下图,如果两条直线组成的锥,分别从直线上选两点,则亮点的线性组合不一定在这两条直线上。
对于凸锥,其中两个重要的实例为Norm cone和Normal cone,接下来着重介绍这两个凸锥的概念。
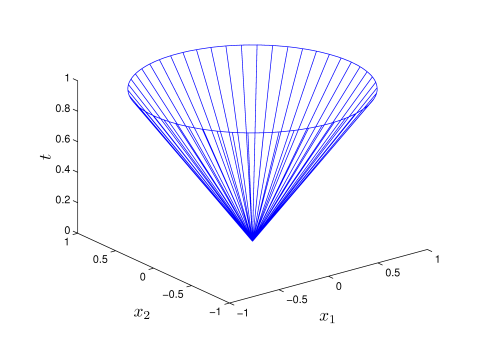
Norm cone是指\(\{(x,t):\parallel x \parallel \leq t\}\),而second-order cone则是使用2阶范数\(norm \parallel \cdot \parallel_2\),如果只看定义的话不太好理解Norm cone是什么,下面给出了matlab仿真得到的三维下的Norm Cone实例:
Normal cone是指给定任意集合\(C\)和点\(x \in C\),\(\mathbb{N}_C(x)=\{g:g^Tx \geq g^Ty\}\),其中\(y \in C\)。无论集合C是否是凸集,满足该定义的点的集合都是Normal cone,其含义是指Normal cone中的点与集合C内的点\(x\)的内积永远大于集合C内任意点与其点x的内积。具体实例如下图,\(x'\)normal cone是集合C边缘切线向量之间的点的集合:
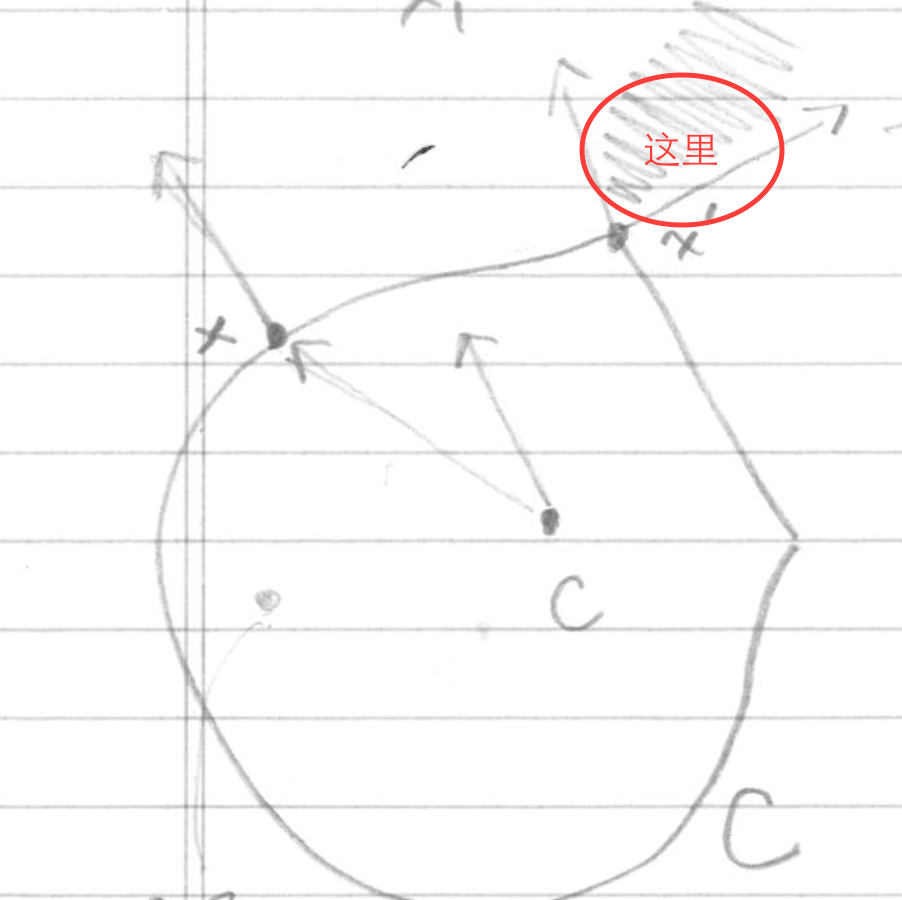
normal cone的定义将会在subgradient descent算法中应用到。
c. 凸集的性质
凸集有两个重要的性质,这对机器学习的分类问题,或者更进一步说,对SVM等算法理论有着重要的支撑作用。
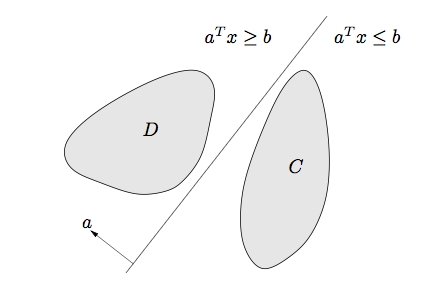
(1)Separating hyperplane理论:两个不相交的凸集之间必然存在一个分割超平面,使得两个凸集可以分开。即如果\(C和D\)都是非空凸集,且\(C \cap D =\emptyset\),则必然存在\(a,b\)使得\(C \subseteq \{x:a^T \leq b\}\) 和 \(D \subseteq \{x:a^Tx \geq b\}\)。如下图:
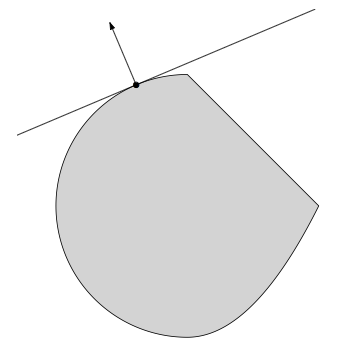
(2)Supporting hyperplane理论:凸集边界上的一点必然存在一个支撑超平面穿过该点,即如果\(C\)都是非空凸集,\(x_0 \in bd(C)\),那么必然存在一个超平面\(a\),使得\(C \subseteq \{x:a^Tx \leq a^Tx_0\}\),如下图:
d. Operations preserving convexity
凸集经过以下几个操作,仍会是凸集:
(1)Intersection: 凸集交集仍然是凸集。
(2)Scaling and translation:如果\(C\)都是凸集,那么对于\(\forall a,b\),\(aC+b=\{ax+b:x \in C\}\)仍是凸集。
(3)Affine images and preimages:如果\(f(x)=Ax+b\),\(C和D\)是凸集,那么\(f(C)=\{f(x):x \in C\}\)和\(f^{-1}(D)=\{x:f(x) \in D\}\)仍是凸集。
这里需要注意的是,第二点和第三点的区别在于,第二点仅相对于凸集做了尺度或平移变换,而第三点则是A为矩阵,b为向量,可以对凸集做矩阵变换,这在图像里可以看成是旋转、压缩、或者是降维操作,而不仅仅是简单的平移变换。
4. 凸函数
a. 凸函数的定义
总体而言,凸函数跟凸集的定义和性质基本一致,凸函数的性质都可以通过凸集来证明。
函数\(f\)为凸函数,如果其满足\(f: \mathbb{R} \rightarrow \mathbb{R}\),使得函数\(f\)的定义域为凸集,\(dom(f) \subseteq \mathbb{R}^n\),且\(f(tx+(1-t)y) \leq tf(x)+(1-t)f(y)\),其中\(0 \leq t \leq 1\)。也就是说凸函数上任意两点的连线都在两点区间的函数之上。具体表现为下图:
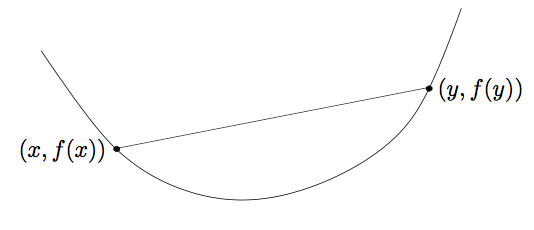
当然,如果函数\(f\)为凸函数,那么相应的\(-f\)则为凹函数。
如果凸函数满足\(f(tx+(1-t)y) < tf(x)+(1-t)f(y)\),其中\(0 < t < 1\),则该函数为严格凸函数(strictly convex);如果严格凸函数还满足\(\forall m > 0: f- \frac{m}{2} \parallel x \parallel_2^2\),则该函数为强凸函数(strongly convex),即函数\(f\)至少是像二次函数一样的凸函数。所以,根据定义,强凸函数一定是严格凸函数,严格凸函数一定是凸函数,反之,则不成立。
例如:单变量函数中的指数函数\(e^{ax}\)、仿射函数\(a^Tx+b\)、二次函数\(\frac{1}{2} x^TQx+b^Tx+c\)(其中\(Q \succeq 0\)半正定)、平方误差函数\(\parallel y-Ax \parallel_2^2\)、p-范数函数\(\parallel x \parallel_p= (\sum_{i=1}^n x_i^p)^{1/p}\)、Indicator function和Max function(\(f(x)=max{x_1, \ldots, x_n}\))均是凸函数,相反,对数函数则为凹函数。其中,Indicator function定义为:
\begin{equation}
I_C(x)=
\begin{cases}
0 \quad x \in C \
\infty \quad x\notin C
\end{cases}
\end{equation}
b. 凸函数的性质
与凸集类似,凸函数具有以下的性质:
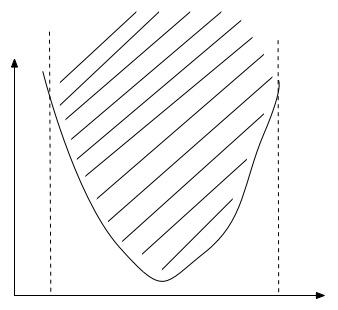
(1)Epigraph characterization:函数\(f\)为凸函数当且仅当,它的epigraph(\(epi(f)=\{(x,t) \in dom(f) \times \mathbb{R}: \, f(x) \leq t\}\))为凸集。其中,函数的epigraph是指在函数上方的所有点的集合,如下图所示,我们可以绘制图像的曲线并采用该方法来确定一个函数是否属于凸函数:
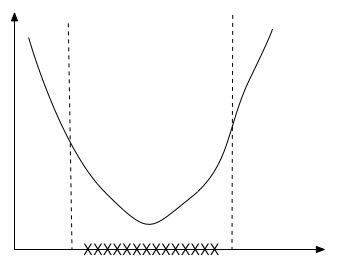
(2)Convex sublevel sets:如果函数\(f\)为凸函数,那么它的sublevel sets(\(\{x \in dom(f): \, f(x) \leq t\}\))为凸集,反之,则不成立。如下图,函数值域小于t的下方的定义域区间(XXX位置)为凸集。
(3)First-order characterization:如果函数\(f\)可微,那么当且仅当\(dom(f)\)为凸集,且对于\(\forall x,y \in dom(f)\),使得\(f(y) \geq f(x)+\nabla f(x)^T(y-x)\),则函数\(f\)为凸函数。这一点很易于理解,即在函数某点切线上的点的值小于该点在函数上的值,如下:
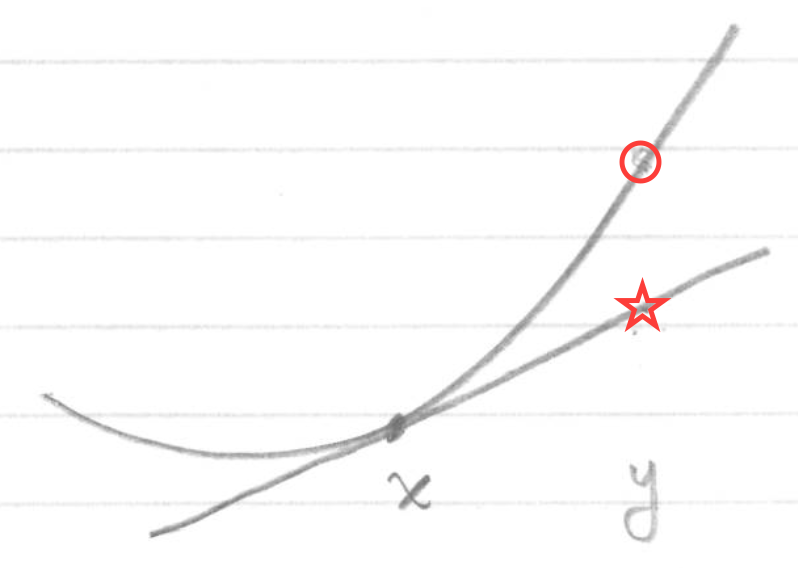
根据凸函数一阶导的性质,我们可以看出,如果当我们找到某一点使得\(\nabla f(x)=0\),那么就会使得函数上所有点\(f(y) \geq f(x)\),即点\(f(x)\)为函数的极小值。这一点,对于接下来将要介绍的优化问题极为重要,阐明我们求解函数极小值的方法。
(4)Second-order characterization:函数\(f\)二阶可微,那么当且仅当\(dom(f)\)为凸集,且对于\(\forall x \in dom(f)\),使得\(\nabla^2 f(x) \succeq 0\),则函数\(f\)为凸函数。
(5)Jensen’s inequality:如果函数\(f\)为凸函数,则\(f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)])\)
c. 凸函数变换
与凸集类似,凸函数经过一些变换后仍能为凸函数,例如:
(1)Nonnegative linear combination;
(2)Pointwise maximization:如果\(\forall s \in S, \, f_s\)为凸函数,那么\(f(x)=max_{s \in S} f_s(x)\)仍为凸函数;
(3)Partial minimization:如果\(g(x,y)\)是凸函数,集合C也为凸集,那么\(f(x)=min_{y \in C} \, g(x,y)\)仍为凸集;
(4)Affine composition:如果函数\(f\)为凸函数,那么经过矩阵变换的函数\(g(x)=f(Ax+b)\)也为凸函数。
5. softmax函数
实例:对于softmax函数,作为机器学习中logistic回归的泛化形式,也成为log-sun-exp函数,什么是softmax函数呢?如何证明该函数为凸函数呢?
假设函数\(g(x)=log \sum_{i=1}{k} e^{a_i^Tx+b_i}\),从表面上可以看出该函数就像估计函数\(max_{i=1,\ldots,k}(a_i^Tx+b_i)\)的最大值,为什么呢?如果\(\forall i, \, a_i^Tx+b_i\),则会得到k个数值,如果其中某一个数值比较大,那么通过指数运算会放大该数值在求和运算中的比例,导致求和运算的最终结果受到该较大数值的影响,所以再求对数缩小数值,最后求得的结果基本上就类似于找到\(a_i^Tx+b_i\)的最大值。但是与直接求最大值不同,该函数是光滑函数,便于运用优化算法求解,因此称为softmax函数。
接下来证明为什么log-sun-exp函数是凸函数:
首先,利用之前提到的affine composition,我们可以知道如果\(f(x)=log(\sum_{i=1}{n}e^{x_i})\)为凸函数,那么softmax肯定为凸函数;
然后,利用凸函数的二阶微分的性质,计算\(f(x)=log(\sum_{i=1}{n}e^{x_i})\)的一阶微分和二阶微分:
\[\nabla_i f(x)=\frac{e^{x_i}}{\sum_{l=1}^n e^{x_l}}\] \[\nabla_{ij}^2 f(x)=\frac{e^{x_i}}{\sum_{l=1}^n e^{x_l}}l{i=j}-\frac{e^{x_i}e^{x_j}}{(\sum_{l=1}^n e^{x_l})^2}=diag(z)-zz^T\]其中,\(z_i=e^{x_i}/(\sum_{l=1}^n e^{x_l})\),通过计算我们可以获得\(\nabla^2 f(x)\)为diagonally dominant矩阵,diagonally dominant是指矩阵\(A\),满足\(A_{ii} \geq \sum_{i \neq j} \mid A_{ij}\mid\),即矩阵对角线上的元素大于该行非对角线元素之和。
因此,证明该矩阵是半正定p.s.d.的(positive semidefinite)。满足上面介绍的凸函数性质的第四点,因此,该softmax函数为凸函数。
Ryan还提到一个例子,这个例子我就不详细阐述为什么是凸函数,大家可以根据上面讲解的知识来判断下面的函数是否是凸函数:
\[max\{log(\frac{1}{(a^Tx+b)^7)}, \parallel Ax+b \parallel_1^3 \}\]