1. 凸优化问题
优化问题的定义为:
\begin{split}
\min \limits_{x \in D} \quad & f(x) \
subject \, to \quad & g_i(x) \leq 0, \, i=1, \ldots, m \
& h_j(x)=0, \, j=1, \ldots, r
\end{split}
其中,\(D=dom(f) \cap \bigcap_{i=1}^m dom(g_i) \cap \bigcap_{j=1}^pdom(h_j)\)。
-
f被称为目标函数(objective or criterion function);
-
g被称为约束函数(inequality constraint function);
-
满足\(g_i(x) \leq 0\)且\(h_j(x)=0\)的点称为可行解(feasible point);
-
所有可行解中函数\(f(x)\)最小的点称为最优值(optimal value),记为\(f^{\ast}\);
-
使得函数\(f(x)\)取得\(f^{\ast}\)的点\(x\)称为最优解(optimal point、solution或minimizer),当然,不是所有凸函数都存在最优解,即解为空,例如直线就不存在;
-
如果点\(x\)满足\(f(x) \leq f^{\ast} + \epsilon\),则称点\(x\)为\(\epsilon-suboptimal\)解。
凸优化问题相对优化问题的定义而言,要求函数\(f\)和\(g_i(x)\)是凸函数,\(h_j(x)=a_j^Tx+b_j\)是仿射函数(\(Ax+b=0\))。
对于仿射集和凸集的差别在凸优化-凸集一文也做了分析,二者的差别就在于凸集是线段而仿射集是直线(一维情况下)。很明显,求解凸函数的极小值(convex minimization)和凹函数的极大值(concave maximization)都是凸优化问题(convex optimization problem)。
2. 凸优化解的集合
我们定义凸优化解的集合(Convex solution sets)为\(X_{opt}\),记为:
\begin{aligned}
X_{opt} = \quad & argmin \, f(x) \
& subject \, to \, g_i(x) \leq 0, \, i=1, \ldots, m\
& Ax=b
\end{aligned}
- 凸优化解的集合有一个关键性质就是凸优化解的集合必为凸集。因为,如果凸优化问题不存在最优解,那么解空间为空集,为凸集;如果凸优化问题仅存在一个解,那必定为多维上的一点,而空间上的一点属于凸集;如果存在两个解,那么必定存在一条线段或者一个平面的解的集合,而线段或者平面都是凸集。接下来,就证明为什么存在两个解,就必然会存在多个解:
证明:假设\(x,y\)都是优化问题的解,那么对于\(\forall \theta\),其中\(1 \leq \theta \leq 1\),则:
-
\(g_i(\theta x + (1 - \theta)y) \leq \theta g_i(x)+(1-\theta)g_i(y) \leq 0\);
-
\(A(\theta x + (1 - \theta)y)=\theta Ax+(1-\theta)Ay=b\);
-
\(f(\theta x + (1 - \theta)y) \leq \theta f(x) + (1-\theta)f(y) = \theta f_{\ast} + (1-\theta)f_{\ast}=f_{\ast}\)。
因此,点\(\theta x + (1 - \theta)y\)也是优化问题\(argmin \, f(x)\)的一个解,所以点\(x,y\)之间必然存在两点连线上的任意点都是优化问题的最优解。故,凸优化问题解的集合为凸集。也就意味着如果凸优化问题存在两个包含两个以上的解时,那么其必定包含无数个解。对于这一点,其实不是特别好想象。
- 凸优化解的集合还有另外一个性质就是:如果优化函数为严格凸函数,那么它的最优解必是唯一的,即解空间\(X_{opt}\)只包含一个元素,如二次优化问题。
3. 凸优化问题实例:LASSO
熟悉机器学习算法里面的线性回归或者逻辑回归的同学因该明白LASSO问题,其定义为:
\begin{split}
\min \limits_{\beta \in \mathbb{R}^p} \quad & \parallel y-X\beta \parallel_2^2 \
subject \, to \quad & \parallel \beta \parallel_1 \leq s
\end{split}
LASSO是Tibshirani(对就是Tibshirani)在1996年JRSSB上的一篇文章上《Regression shrinkage and selection via lasso》提出的。所谓lasso,其全称是least absolute shrinkage and selection operator,其含义是在限制了\(\sum \parallel \beta \parallel_1 \leq s\)的情况下,求使得残差平和达到最小的参数的估值。Tibshirani指出,对于回归算法,当\(s\)足够小的时候,会使得某些回归系数的估值是0,可以起到变量选择的作用,是逐步回归的一种表现。
因此,对于LASSO算法,其是否是凸优化问题?它的解集合是否是唯一的点?
答案是,LASSO问题是凸优化问题,因为\(f(x)=\parallel y-X\beta \parallel_2^2\)和\(g(x)=\parallel \beta \parallel_1 - s\)均是凸函数,因此该问题为凸优化问题;如果样本数目\(n\)大于特征数目\(p\),且X满秩,那么\(\nabla^2 f(\beta)=2X^T X \succeq 0\),关于\(\beta\)二阶微分恒为半正定p.s.d.,因此,解是唯一的;但是,如果样本数目\(n\)小于特征数目\(p\),那么会造成高维特征空间上的维数灾难问题,此时,X为奇异矩阵,则解不唯一。
另一个实例是SVM算法,SVM算法的理论部分我就不多介绍了,会在机器学习算法篇章中对SVM做着重介绍,如果我们记SVM为:
\begin{split}
\min \limits_{\beta, \beta_0, \xi} \quad & \frac{1}{2}\parallel \beta \parallel_2^2 + C \sum_i^n \xi_i \
subject \, to \quad & \xi_i \geq 0, \, i=1, \ldots, n\
& y_i(x_i^T \beta+\beta_0) \geq 1-\xi_i, \, i=1,\ldots,n
\end{split}
其中,\(\frac{1}{\parallel \beta \parallel}\)为下图两个虚线边界的距离,\(\xi\)为引入分类错误的代价,代表下图错分样本点距正确分类边界的距离。具体如下图:

那么,该问题是否为凸优化问题呢?它的解是否是唯一?
答案是,SVM目标函数是凸优化问题,但是,它的解并不唯一,因为它不是严格凸函数。有兴趣的同学可以留言来解释为什么SVM是凸优化问题!
4. 局部最小值就是全局最小值
局部最优解的定义为:如果\(\exists \, R > 0\),使得\(f(x) \leq f(y)\),其中y满足\(\parallel x-y \parallel_2 \leq R\),则点x为优化问题的局部最优解(locally optimal)。
对于凸优化问题,凸函数有一个特别的性质,即局部最优解是全剧最优解(local minima are global minima),即如果\(x \in D\),同时\(x\)满足所有约束,那么对于局部\(y,\parallel x-y \parallel_2 \leq \rho\),当\(f(x) \leq f(y)\)时,对于所有可行解\(y, f(x) \leq f(y)\)。相反,非凸优化问题则不具有该性质,如下图所示。
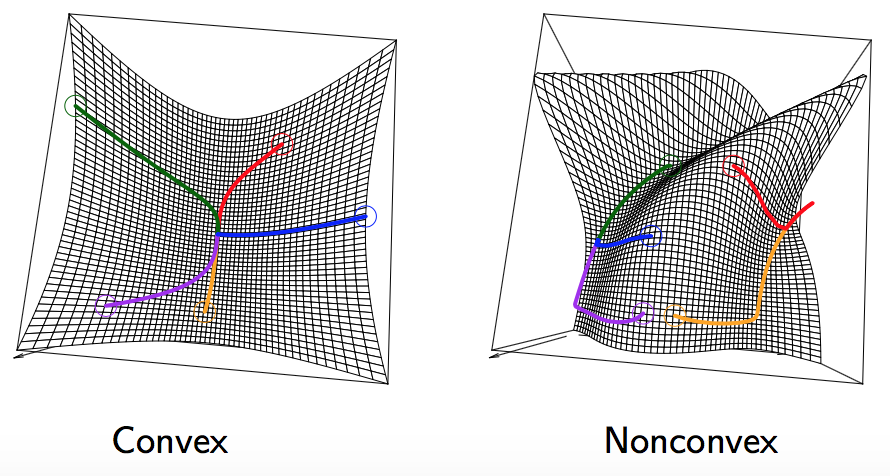
那么我们需要证明的是为什么凸优化问题的局部最优值就是全局最优值?
证明:这里,我们采用反证法来证明该理论,假设x为凸优化问题的局部最优解,意味着函数在\(\rho\)范围内的点的值都小于\(f(x)\)。如果我们假设定理是错误的,那么必然存在一点\(z\),使得\(f(z) < f(x)\),且\(\parallel z-x \parallel_2 > \rho\)。
此时,假设存在一点\(y\),使得\(y=tz+(1-t)x\),其中\(t \in [0,1]\),那么:
-
\(y \in D\),因为\(x \in D\),同时\(z \in D\),二者线性组合也必然存在于D;
-
\(g_i(y)=tg_i(z)+(1-t)g_i(x) \leq 0\),因为\(g_i(z),g_i(x) \leq 0\);
-
\(h_i(j)=a_j^T(tz+(1-t)x)+b_j=a_j^T(tz+(1-t)x)+tb_j+(1-t)b_j=0\)。
因此,意味着\(y\)同样也是是凸优化问题的可行解。
然后,因为点\(y\)在\(t \in [0,1]\)内均成立,所以我们可以假设\(t\)足够小,但大于0,使得\(y\)可以落在点\(x\)以\(\rho\)为半径的圆内,这时,对于凸优化问题中可行解的两个点\(z,x\)之间的点\(y\),我们可以得到如下公式:
\[f(y) \leq tf(z) + (1-t)f(x)\]又因为\(t \rightarrow 0\),且之前假设\(f(z) < f(x)\),所以\(tf(z) < tf(x)\),因此\(f(y) < f(x)\),这就与之前最开始假设x为局部最优解的定义相违背,因此,我们最终证明得到local minima are global minima。
5. 凸优化问题的一些性质和Trick
- First-order optimality condition:对于凸优化问题\(min \, f(x), \, subject \, to \, x \in C\),如果函数\(f\)可微,那么当且仅当满足下式时,可行解(feasible point)\(x\)为最优解。
- Partial optimization:如果\(x=(x_1,x_2) \in \mathbb{R}^{n_1+n_2}\),那么优化问题
\begin{split}
\min \limits_{x_1,x_2} \quad & f(x_1,x_2) \
s.t. \quad & g_1(x) \leq 0, \
& g_2(x_2) \leq 0
\end{split}
等价于:
\begin{split} \min \limits_{x_1} \quad & \tilde{f}(x_1) \\ s.t. \quad & g_1(x_1) \leq 0 \end{split}
其中\(\tilde{f}(x_1)=min\{ f(x_1,x_2):g_2(x_2) \leq 0 \}\);
SVM采用的hinge loss就是利用的partial optimization的思想。如果我们把SVM优化问题的目标函数记为:
\begin{split}
\min \limits_{\beta,\beta_0,\xi} \quad & \frac{1}{2}\parallel \beta \parallel_2^2 + C \sum_i^n \xi_i \
subject \, to \quad & \xi_i \geq 0, \, y_i(x_i^T \beta + \beta_0) \geq 1-\xi_i
\end{split}
那么我们可以将约束改写为\(\xi_i \geq max\{0, \, 1-y_i(x_i^T \beta + \beta_0) \}\),SVM在优化过程中选用的hinge form就是将约束中的大于等于改写为等于,即:
\[\xi_i = max \{ 0, \, 1-y_i(x_i^T \beta + \beta_0) \}\]因此,优化目标函数就变为:
\[\min \limits_{\beta,\beta_0} \quad \frac{1}{2}\parallel \beta \parallel_2^2+C \sum_{i=1}^n[1-y_i(x_i^T \beta + \beta_0)]_+\]上式就是SVM求解目标函数的最终形式,可称为hinge form of SVMs。
- Transformations of variables:如果函数\(h\)为单调递增函数,那么凸优化问题等价于:
优化方法中的最大似然估计MLE就采用log函数对目标函数进行变换,就是采用的这个思想。
- Introducing slack variables:凸优化可以通过引入松弛因子(slack variables)来消除约束(constraints)中的不等式,我们可以把凸优化问题转换为:
\begin{split}
min \quad & f(x) \
subject\, to \quad & s_i \geq 0, i=1,\ldots,m\
& g_i(x)+s_i=0, i=1,\ldots,m\
& Ax=b
\end{split}
SVM算法都引入slack variables来允许训练误差的出现,防止模型过拟合。
5. 凸优化问题分类
凸优化问题根据目标函数和约束函数的形式分为:
- linear programs:线性规划;
- Quadratic programs:二次规划;
- Semidefinite programs:半正定规划;
- Cone programs:锥规划。
Ryan教授给了一个非常形象的例子来解释凸优化问题在优化问题领域的位置,以及以上几种优化问题间的关联关系,如下图:
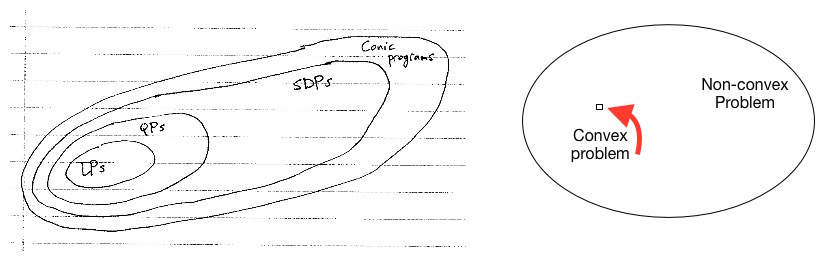
线性规划问题(LPs)定义是优化问题满足以下形式,线性规划的实例包括diet problem, transportation problem, basis pursuit和Dantzig selector等:
\begin{split}
\min \limits_{x} \quad & c^Tx \
subject \, to \quad & Dx \leq d \
& Ax =b
\end{split}
二次规划问题(QPs)定义是优化问题满足以下形式,二次规划的实例包括portfolio optimization, lasso, SVM等:
\begin{split}
\min \limits_{x} \quad & C^Tx+\frac{1}{2}x^TQx \
subject \, to \quad & Dx \leq d \
&Ax=b
\end{split}
其中,\(Q \succeq 0\)是半正定。这里需要注意的是,当Q不是半正定的时候,上述问题则不属于凸优化问题。同样,当\(Q=0\)时,二次规划问题就变为线性规划问题。
半正定规划问题(SDPs)定义是优化问题满足以下形式:
\begin{split}
\min \limits_{x} \quad & c^Tx \
subject \, tp \quad & x_1F_1+\ldots +x_nF_n \succeq F_0 \
&Ax=b
\end{split}
其中,\(F_j \in \mathbb{S}^d\),同时,\(A \in \mathbb{R}^{m \times n}\)。从上面的定义可以看出,和线性规划的定义基本一样,这里SDPs要求\(F_j\)为矩阵,而LPs为向量,所以线性规划一定隶属于半正定规划的一个特例。