1. 引言
凡心所向,素履所往,生如逆旅,一苇以航。
很高兴阿森纳能在欧冠上战胜拜仁,在虎扑上看到这样的一句话,颇有感触,借来作为这篇博文的开始,生活中我们需要一些勇气去追寻自己的理想。回到本篇内容上,对偶是个神奇的东西,从文学角度而言,对偶和对仗属于一种修辞手法,即用字数相等,语义对称的方法来表征想法或抒发情感。“凡心所向,素履所往,生如逆旅,一苇以航”或者“棋逢对手,将遇良才”都可看成是一种对偶。
但是,本文是要阐述在数学问题上的对偶问题,它是优化问题中非常重要的方法,类似于文学的对偶,也是一种配对方式,只不过是将某种数学结构\(A\)转换为另一种对等的数学结构\(B\)。在优化问题中,可以将非凸问题转化为凸优化问题进行求解。虽然文学上和数学上表达对偶的意思相差甚远,但是我觉得二者在各自领域的重要性是可以比拟的。
update: 在完成本篇博文时,拜仁5:1战胜阿森纳,小组出线堪忧。
说到对偶问题,我们先从线性规划谈起,考虑以下简单的线性规划(LP)问题,我们如何求得函数的下界:
\begin{equation}
\begin{split}
\min \limits_{x,y} & \quad x+3y \
subject \, to & \quad x+y \geq 2 \
& \quad x, y \geq 0
\end{split}
\end{equation}
实际上,我们可以从两个角度求解这个问题:首先,我们可以采用图解法找寻问题的解。下图中蓝线代表\(x+3y=0\)的直线,黑线表示约束\(x+y=2\),我们可以通过移动蓝线的位置,使得蓝线右上方的所有点\(x\)和\(y\)满足约束,因此,直至蓝线移至红线位置才能满足上述LP问题的约束,而黄线代表的\(x+3y=0.6\)则不能满足约束,因为点\((x,y)=(0,0.2)\)不满足\(x+y \geq 2\)的条件。
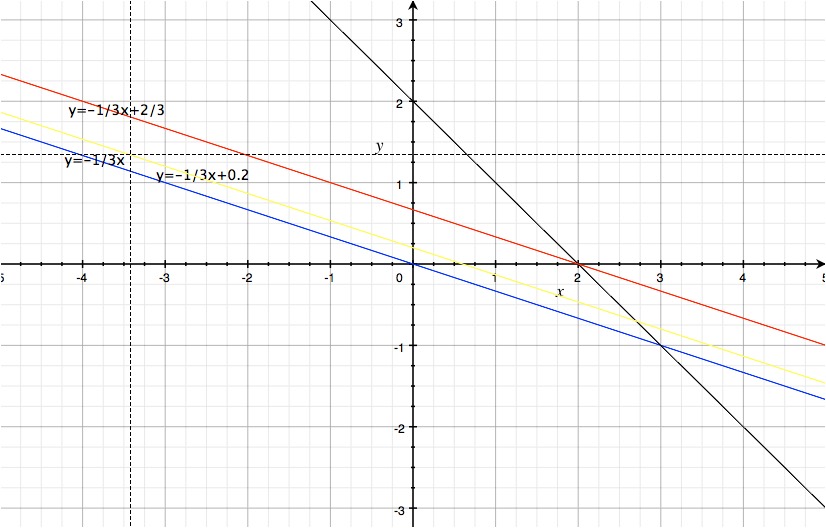
因此,通过作图,移动目标函数直线的位置,我们都能获得上述LP问题的最小值,即为2。
同样,我们也可以利用以下变换获得目标函数的最小值:
\begin{equation}
\begin{split}
& \quad x+y \geq 2 \
& + \quad 2y \geq 0 \
& = \quad x+3y \geq 2
\end{split}
\end{equation}
很明显,\(x+3y\)的最小值为2。如果我们泛化上述LP问题为:
\begin{equation}
\begin{split}
\min \limits_{x,y} & \quad px+qy \
subject \, to & \quad x+y \geq 2 \
& \quad x, y \geq 0
\end{split}
\end{equation}
我们如何求解?按照变换方法,我们可以获得:
\begin{equation}
\begin{split}
\, & \quad a(x+y) \geq 2a \
& + bx \geq 0 \
& + cy \geq 0 \
& = (a+b)x+(a+c)y \geq 2a
\end{split}
\end{equation}
因此,我们只要使得\(a+b=p\),同时\(a+c=q\),那么上述问题的最优解为\(2a\)。这里\(2a\)为\(px+qy\)的下界,即\(px+qy \geq 2a\)永远成立,所以,我们应当使得下界最大化,找到满足约束条件\(a+b=p\)和\(a+c=q\)的最大值\(a\),才能求得左式的最小值。
综上所述,上述LP问题就转换为求下面形式的最大值:
\begin{equation}
\begin{split}
\max \limits_{a,b,c} & \quad 2a \
subject \, to & \quad a+b=p \
& \quad a+c=q \
& \quad a,b,c \geq 0
\end{split}
\end{equation}
我们即称上述变换为原问题(Primal)的对偶(dual)问题。
2. 线性规划问题的对偶问题
对于一般形式的线性规划问题:
\begin{equation}
\begin{split}
\min \limits_{x \in \mathbb{R}^n} & \quad c^Tx \
subject \, to & \quad Ax = b \
& \quad Gx \leq h
\end{split}
\end{equation}
我们可以获得其对偶问题:
\begin{equation}
\begin{split}
\max \limits_{u \in \mathbb{R}^m,\, v \in \mathbb{R}^r} & \quad -b^Tu-h^Tv \
subject \, to & \quad -A^Tu -G^Tv = c \
& \quad v \leq 0
\end{split}
\end{equation}
因为:
\begin{equation}
\begin{split}
\, & \quad -u^TAx = -b^Tu \
& + -v^TGx \geq -h^Tv \
& = (-A^Tu - G^Tv)^Tx \geq -b^Tu - h^Tv
\end{split}
\end{equation}
如果\(c\)满足\(c=-A^Tu - G^Tv\),那么我们可以获得LP问题解得下界\(-b^Tu - h^Tv\)。
3. 拉格朗日函数
根据LP对偶问题的构建方法,我们可以令\(L(x,u,v):= c^Tx + u^T(Ax - b) + v^T(Gx - h)\),其中\(v \geq 0\)。因为,\(Ax - b =0\)且对于\(\forall v,\, v^t(Gx - h) \leq 0\),因此,\(L(x,u,v) \leq c^Tx\)。
如果我们假设集合\(C\)为原问题的解集合,\(f^{\star}\)为最优解,那么对于任意\(u\)和\(v \geq 0\),我们可以获得:
\[f^{\star} = \min \limits_{x \in C} c^Tx \geq \min \limits_{x \in C} L(x,u,v) \geq \min \limits_{x} L(x,u,v) = \min \limits_{x} (c + u^TA +v^TG)^Tx - u^Tb - v^Th :=g(u, v)\]对于上式,\(\min \limits_{x} L(x,u,v)\)为关于\(x\)的线性函数,因此,如果\(c + u^TA +v^TG\)不等于0,那么对于所有\(x\),函数\(L(x,u,v)\)最小值为\(-\infty\),所以,想要保证求得原问题的最小值,我们必须保证\(c + u^TA +v^TG = 0\),此时,\(g(u,v) = \min \limits_{x} L(x,u,v) = -b^Tu - h^Tv\)。
综上所述,我们可以获得函数\(g(u, v)\)的一般形式:
\begin{equation}
g(u,v) =
\begin{cases}
-b^Tu - h^Tv & if \, c = - u^TA - v^TG \
-\infty \quad & otherwise
\end{cases}
\end{equation}
现在我们最大化函数\(g(u, v)\),获得原问题的紧致下界(tightest bound),这与上面之前定义的对偶问题完全一致。同时,这种变换或者解释方法可以适用于任意优化问题上,甚至是非凸优化问题。我们可以根据有约束的优化问题获得函数\(L(x,u,v)\),然后求解\(\min \limits_{x} L(x,u,v)\)得到函数\(g(u,v)\),即为原问题的对偶问题。
综上所述,对于一般有约束的优化问题,如下:
\begin{equation}
\begin{split}
\min \limits_{x} & \quad f(x) \
subject \, to & \quad h_i(x) \leq 0, \, i=1,\ldots,m \
& \quad l_i(x) = 0, \, j=1,\ldots,r
\end{split}
\end{equation}
无论\(f(x)\)是否为凸函数,我们都可以定义拉格朗日函数(Lagrangian)为:
其中,\(u \geq 0\),同时,定义朗格朗日函数\(L(x,u,v) = -\infty \, for \, u < 0\)。意味着对于任意可行解\(x\),且\(u \geq 0\),\(f(x) \geq L(x,u,v)\)。下图是Boyd凸优化一书中给出拉格朗日函数的实例图:
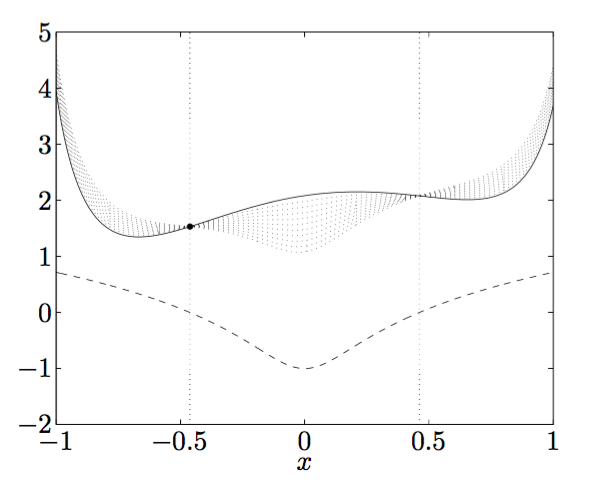
图中,实线表示函数\(f(x)\),虚线表示函数\(h(x)\),为约束,点线表示不同\(u,v\)下的函数\(L(x,u,v)\)。根据约束信息,我们可以获得函数可行解域为[-0.46,0.46],在该区域下\(f(x) \geq L(x,u,v)\)。
同样,如果我们假设集合\(C\)为原问题的解集合,\(f^{\star}\)为最优解,那么对于任意\(x\),最小化函数\(L(x,u,v)\)可以获得函数下界:
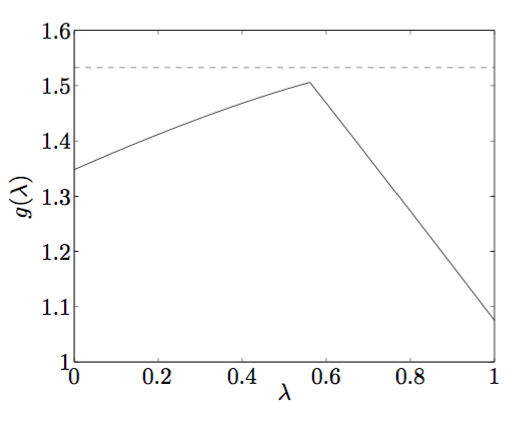
\[f^{\star} = \min \limits_{x \in C} c^Tx \geq \min \limits_{x \in C} L(x,u,v) \geq \min \limits_{x} L(x,u,v) := g(u, v)\]我们称函数\(g(u,v)\)为拉格朗日对偶函数(Lagrange dual function),对于对偶可行解\(u,v\),它给定了\(f^{\star}\)的下界(其中\(u \geq 0\)),我们最大化\(g(u,v)\),即可获得\(f^{\star}\)的逼近解。如下图,虚线表示原问题最优解\(f^{\star}\),实线表征不同\(u\)下\(g(u)\)的值,可以看出,最大化\(g(u)\)可以逼近\(f^{\star}\),(图中的\(\lambda\)为\(u\)):
3. 对偶函数实例:二次规划
这里,我们用二次函数的优化问题作为一个例子来说明如何获得拉格朗日对偶函数,我们定义二次规划为:
\begin{equation}
\begin{split}
\min \limits_{x} & \quad \frac{1}{2}x^TQx + c^Tx \
subject \, to & \quad Ax = b \
& \quad x \geq 0
\end{split}
\end{equation}
其中,\(Q \succ 0\)。
因此,拉格朗日函数为\(L(x,u,v)=\frac{1}{2}x^TQx + c^Tx -u^Tx + v^T(Ax-b)=\frac{1}{2}x^TQx +(c + v^TA -u)^Tx + v^Tb\),对于形如\(ax^2+bx+c\)的二次函数,我们可以获得函数的根为\(x=-\frac{b}{2a}\),即\(x=(c - u +A^Tv)Q^{-1}\),函数\(L(x,u,v)\)的最小值为\(-\frac{1}{2} (c - u +A^Tv)^TQ^{-1}(c - u +A^Tv)-b^Tv\)。
所以,我们可以获得拉格朗日对偶函数\(g(u,v)= \min \limits_{x \in \mathbb{R}^n} L(x,u,v) = -\frac{1}{2} (c - u +A^Tv)^TQ^{-1}(c - u +A^Tv)-b^Tv\),其中\(u \geq 0\),\(v\)为任意值。
4. 拉格朗日对偶问题
拉格朗日对偶问题是指对于原问题:
\begin{equation}
\begin{split}
\min \limits_{x} & \quad f(x) \
subject \, to & \quad h_i(x) \leq 0, \, i=1,\ldots,m \
& \quad l_i(x) = 0, \, j=1,\ldots,r
\end{split}
\end{equation}
我们通过构造对偶函数\(g(u,v)\),然后最大化该对偶函数的优化问题,即:
\begin{equation}
\begin{split}
\max \limits_{u,v} & \quad g(u,v) \
subject \, to & \quad u \geq 0
\end{split}
\end{equation}
对于原问题的对偶问题,它有两个重要性质:
-
弱对偶性(weak duality):无论是凸优化或非凸优化原问题,\(f^{\star} \geq g^{\star}\)(因为\(f(x) \geq g(u,v)\)); -
对偶问题是凸优化问题:无论原问题是凸优化还是非凸,因为\(l_j(x)为凸函数\)。
这里需要指出的是,是不是我们可以获得任意原问题的对偶问题,这样就可以采用之前提到过的下降算法等来求解该凸优化问题?
答案是否定的,虽然无论原问题为何种形式,其对偶问题永远是凸优化问题,但是这里的关键并不是说不能用下降算法求解,而是我们对于非凸问题一般无法获得或者较难获得其对偶问题的表达式\(g(u,v)\),这就限制了我们对于非凸优化问题的求解方法。
对于对偶问题,弱对偶性永远成立,更进一步,如果我们可以获得\(f^{\star} = g^{\star}\),那么我们就可以保证求解对偶问题获得的最优解可以变换为原问题的最优解。我们将\(f^{\star} = g^{\star}\)形式成为强对偶性(strong duality)。
Slater’s condition:如果原(primal)问题为凸优化问题(即:\(f, h_1,\ldots,h_m\)为凸函数,\(l_1,\ldots,l_r\)是仿射函数),同时存在至少一个可行解满足\(h_1(x) <0, \ldots,h_m(x) <0, l_1(x)=\ldots=l_r(x)=0\),那么该问题的强对偶性成立,即\(f^{\star} = g^{\star}\)。
因此,根据强对偶性的定义和成立条件,我们可以获得以下性质:
-
LP问题对偶问题的对偶问题为原问题(the dual of the dual LP is the primal LP);
-
如果LP问题存在可行解,那么LP问题满足具有强对偶性;
根据强对偶性定义,我们可以衍伸出对偶间隙(duality gap)的定义,对偶间隙是指\(f(x)-g(u,v)\),很明显,\(f(x)-f^{\star} \leq f(x) - g(u,v)\),因此,如果对偶间隙为0,那么\(f(x)-f^{\star} = f(x) - g^{\star}\),这时,\(u,v\)和对应获得的\(x\)分别为对偶问题和原问题的最优解。
对偶间隙的最大用途是作为算法停止迭代的条件,即如果我们想要保证\(f(x)-f^{\star} \leq \epsilon\),那么需要\(f(x)-g(u,v) \leq \epsilon\)。
5. 对偶问题实例:SVM对偶问题
之前我们提到过,SVM问题是:
\begin{equation}
\begin{split}
\min \limits_{\beta,\beta_0,\xi} & \quad \frac{1}{2}\parallel \beta \parallel_2^2 + C \sum_i^n \xi_i \
subject \, to & \quad \xi \geq 0, \, i=1,\ldots,n \
& \quad y_i(x_i^T\beta + \beta_0) \geq 1 - \xi_i, \, i=1,\ldots,n
\end{split}
\end{equation}
引入对偶变量(dual variables),\(v,w \geq 0\),我们可以构建拉格朗日函数:
\[L(\beta, \beta_0, \xi, v, w) = \frac{1}{2} \parallel \beta \parallel_2^2 + C \sum_{i=1}^{n} \xi - \sum_{i=1}^{n}v_i \xi + \sum_{i=1}^{n}w_i(1- \xi - y_i(x_i^T\beta + \beta_0))\]如想获得拉格朗日对偶函数,我们需要对\(\beta, \beta_0, \xi\)求导。
(1)对\(\beta_0\)求导,我们获得:\(\frac{\partial L}{\partial \beta_0}=-\sum_{i=1}{n}y_iw_i=w^Ty\)。因为拉格朗日函数\(L\)是关于\(\beta_0\)的仿射函数,所以\(w^Ty=0\),否则,\(min(L)=-\infty\),即获得约束\(w^Ty=0\);
(2)对\(\xi_i\)求导,我们获得:\(\frac{\partial L}{\partial \xi_i}=-\sum_{i=1}{n}c-v_i-w_i=CI-v-w\)。因为拉格朗日函数\(L\)是关于\(\xi_i\)的仿射函数,所以需要\(CI-v-w=0\),否则,\(min(L)=-\infty\),即获得约束\(w=CI - v\);
(3)对\(\beta\)求导,我们获得:\(\frac{\partial L}{\partial \beta}=(\frac{1}{2}\beta^T \beta - w^T(diag(Y)X)\beta)'\),因此,\(\beta = w^T(diag(Y)X)\)。因为,拉格朗日函数\(L\)是关于\(\beta\)的二次函数,所以存在最小值\(-\frac{1}{2}w^T(diag(y)X)(diag(Y)X)^Tw +I^Tw\)。
综上所述,通过最小化\(\beta, \beta_0, \xi\),我们获得拉格朗日函数\(L(\beta, \beta_0, \xi, v, w)\)的拉格朗日对偶函数\(g(v,w)\):
\begin{equation}
g(v,w) =
\begin{cases}
-\frac{1}{2}w^T(diag(Y)X)(diag(Y)X)^Tw +I^Tw & if \, w^Ty=0,\, w=CI - v \
-\infty \quad & otherwise
\end{cases}
\end{equation}
又因为\(\xi\)为原问题的松弛因子,且\(v \geq 0\),因此我们可以消除对偶问题中的松弛因子\(v\)(slack variable),SVM对偶优化问题就变为:
\begin{equation}
\begin{split}
\max \limits_{w} & \quad -\frac{1}{2}w^T(diag(y)X)(diag(Y)X)^Tw +I^Tw \
subject \, to & \quad 0 \leq w \leq CI, \, w^Ty=0
\end{split}
\end{equation}
如果SVM原问题满足Slater’s Condition,那么SVM具有强对偶性(事实上SVM具有强对偶性),我们可以通过求解对偶问题的最优解,进而获得原问题最优解\(\beta = (diag(Y)X)^Tw\)。