1. 引言
Proximal算法是用于求解凸优化问题的方法之一,当无约束的凸优化问题可微,我们可以用梯度下降算法求解;当无约束的凸优化目标函数不可微,我们可以采用次梯度算法求解;当存在约束时,我们可以采用proximal相关梯度算法求解,这是因为,当目标函数存在约束时,我们可以把约束写入目标函数,但是这时候往往目标函数就从可微变成不可微,例如线性回归加入\(L-1 norm\),记为\(\parallel y- x\beta \parallel_2^2 + \lambda \parallel \beta \parallel_1\),那么很明显,目标函数前半部分为凸且连续可微,但后半部分为凸但不连续可微。因此,proximal算法就是用于求解目标函数形如\(f(x) = g(x) + h(x)\)(其中\(g(x)\)可微而\(h(x)\)不可微)形式无约束问题的下降算法。
虽然,我们仍然可以采用次梯度算法求解上述问题,但是该算法时间复杂度较高,这里所要讲述的proximal method既是可以降低复杂度至\(O(1/\epsilon)\)。
2. Proximal Mapping
对于形如\(f(x) = g(x) + h(x)\)形式的目标函数,如果\(g(x)\)为连续可导的凸函数,而\(h(x)\)仅为凸函数,我们则可以通过proximal mapping将函数映射为\(prox_t(x) = argmin_z \frac{1}{2t} \parallel x - z \parallel_2^2 + h(z)\),转而求解\(prox_t(x)\)的最优解。
-
当\(h(x) = 0\):\(prox_t(x) = argmin_z \frac{1}{2t} \parallel x - z \parallel_2^2 = x\);
-
当\(h(x) = I_C(x)\)(可表征为约束):\(prox_t(x) = argmin_{z \in C} \frac{1}{2t} \parallel x - z \parallel_2^2\);
-
当\(h(x) = \lambda \parallel x \parallel_1\):\(prox_t(x) = argmin_{z} \frac{1}{2t} \parallel x - z \parallel_2^2 + \lambda \parallel z \parallel_1 = S_{\lambda t}(x)\)。
其中,\(S_{\lambda t}(x)\)记为:
\begin{equation}
S_{\lambda t}(x) =
\begin{cases}
x - \lambda t \quad & if \, x > \lambda t \
0 \quad & if \, - \lambda t \leq x \leq \lambda t \
x + \lambda t \quad & if \, x < -\lambda t
\end{cases}
\end{equation}
3. Proximal Gradient Descent
如果\(f\)为可微的凸函数,那么我们可以采用梯度下降算法更新梯度,即\(x^+ = x - t\nabla f(x) = argmin_x f(x)\)。我们对\(f(x)\)做二阶泰勒展开,获得如下梯度下降算法梯度更新表达式:
\[x^+ = argmin_z f(x) + \nabla f(x)^T(z-x)+\frac{1}{2t} \parallel z - x \parallel_2^2\]因此,对于proximal gradient descent算法,我们保持\(f(x) = g(x) + h(x)\)中的\(h(x)\)不动,仅对\(g(x)\)做泰勒展开(因为\(g(x)\)可微),即:
\begin{equation}
\begin{split}
x^+ & = argmin_z g(x) + \nabla g(x)^T(z-x)+\frac{1}{2t} \parallel z - x \parallel_2^2 + h(z)\
& = argmin_z \frac{1}{2t} \parallel z - (x -t \nabla g(x)) \parallel_2^2 + h(z) \
& = prox_t(x - t\nabla g(x))
\end{split}
\end{equation}
通过上式,我们可以获得proximal gradient descent算法梯度更新表达式:
\[x^{(k)} = prox_{t_k} (x^{(k-1)} - t\nabla g(x^{(k-1)}))\]其中,\(k\)为当前迭代次数,为了使得上式和梯度下降形式保持一致,我们可以将上式改写为:
\[x^{(k)} = x^{(k-1)} - t_k G_{t_k}(x^{(k-1)}\]其中 \(G_t(x) = \frac{x - prox_t(x - t\nabla g(x))}{t}\)。
4. 实例(ISTA)
(1) 当\(h = 0\)时,\(prox_t(x) = x\),即\(x^{(k)} = prox_{t_k} (x^{(k-1)} - t\nabla g(x^{(k-1)}))= x^{(k-1)} - t\nabla g(x^{(k-1)})\),为梯度下降算法(gradient descent);
(2) 当\(h = I_C\)时,\(prox_t(x) = argmin_{z \in C} \frac{1}{2t} \parallel x - z \parallel_2^2\),所以该算法对应投影梯度下降算法(projected gradient descent),如下图:
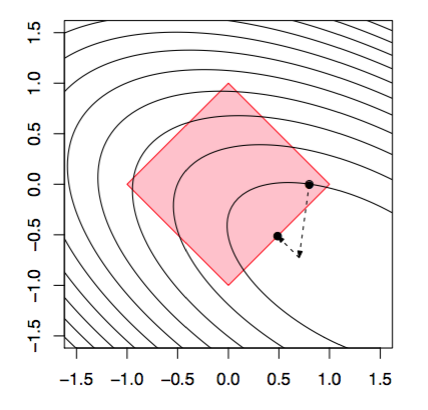
(3) 当\(h(x) = \lambda \parallel x \parallel_1\),问题可理解为LASSO问题,目标函数(lasso criterion)为\(f(\beta) = \underbrace{\frac{1}{2} \parallel y - X\beta \parallel_2^2}_{g(\beta)} + \underbrace{\lambda \parallel \beta \parallel_1}_{h(\beta)}\)。
根据上面介绍的proximal mapping,我们知道上式可写为:
\[prox_t(\beta) = argmin_{z} \frac{1}{2t} \parallel \beta - z \parallel_2^2 + \lambda \parallel z \parallel_1 = S_{\lambda t}(\beta)\]因此,针对L1 norm的proximal gradient descent算法的梯度更新公式为:
\[\beta^+ = S_{\lambda t}(\beta + tX^T(y-X\beta))\]其中,\(\nabla g(\beta) = -X^T(y - X\beta)\)。该方法也称为iterative soft-thresholding algorithm(ISTA)算法。下图是该方法与次梯度算法在迭代次数为1000时目标函数误差结果,从结果可以看出,ISTA算法收敛速度明显优于subgradient method。
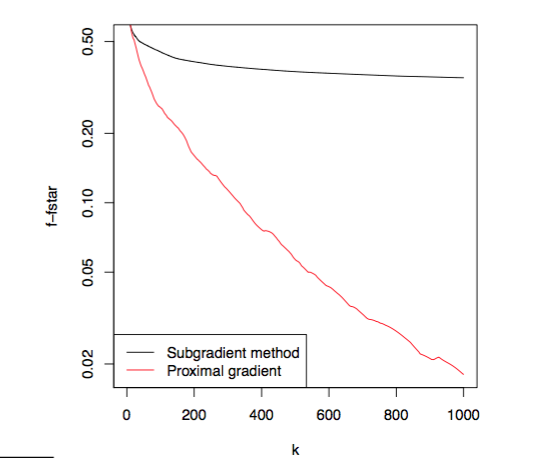
(4) 当\(g = 0\)时,梯度更新公式变为\(x^+ = argmin_z \frac{1}{2t} \parallel x-z \parallel_2^2 + h(z)\),一般我们成为proximal minimization algorithm。
综上所述,我们可以把promixal gradient descent算法看成是梯度下降等算法的一般形式,通过改变\(g\)和\(h\)的定义,我们可以衍伸出不同的下降算法的一般形式。
5. 收敛性分析
对于proximal gradeint descent收敛性分析,我这里就不在给出相关证明,其证明方法与梯度下降和次梯度算法类似,假设\(\nabla g\)是L-Lipschitz,且\(h\)为凸函数,那么固定步长\(t\)的proximal gradeint descent算法收敛性满足:
算法收敛速度为\(O(1/\epsilon)\),因此该算法收敛速度和梯度下降一致,但是,需要注意的是这里收敛速度的指该算法与梯度下降算法在达到同样的\(f(x^{(k)}) - f^{\ast}\)误差时所需要的迭代次数是一致的,不要理解成二者收敛需要的时间是一致的,因为这里的收敛速度不是指的数据结构中得程序步的概念。
与梯度下降算法类似,我们也可以采用Backtracking line search来自动调整每次更新的步长。对于每一次迭代,首先设置\(t=1\),然后判断是否满足\(g(x-tG_t(x)) > g(x) - t\nabla g(x)^T G_t(x) + \frac{t}{2} \parallel G_t(x) \parallel_2^2\),如果满足则进行下一次迭代;如果不满足则压缩(shrink)\(t = \beta t\)。对于采用Backtracking line search的proximal gradient descent算法其收敛速度为:
其中,\(t_{min} = min \{1, \beta/L \}\)。
5. 加速(Acceleration)
Nesterov提出可以对promixal gradient descent算法进行加速,使其收敛速度更快,根据Ryan教授所讲,虽然理论上他可以达到更快的收敛速度,但是一般在优化过程中很少使用加速,转而大多使用warm starts。warm starts通过不断收敛\(\lambda_j\)的值,来逼近最优解。一般情况下,仅需要通过有限的网格搜索,即可获得与acceleration一样的效果。
加速算法一般步骤为:
设定初始值为\(x^{(0)} = x^{(-1)}\),然后对于\(k=1,2,3,\ldots\)重复更新:
\[v = x^{(k-1)} + \frac{k-2}{k+1} (x^{(k-1)} - x^{(k-2)})\] \[x^{(k)} = prox_{t_k} (v- t_k \nabla g(v))\]当\(k=1\)时,与proximal gradient更新一致,随后,在每次更新的时候增加一些冲量(momentum)。下图是次梯度、proximal gradient和Nesterov acceleration在lasso问题上收敛结果的对比。
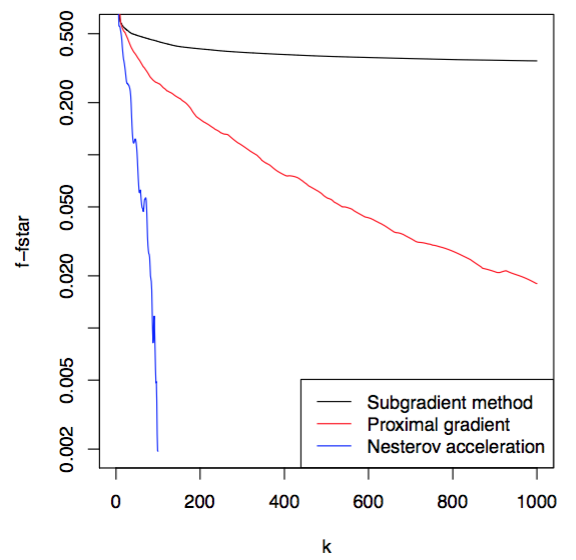
需要指出的是,Nesterov acceleration算法并不算是下降算法,其收敛过程有点类似涟漪(ripples)的形状,不是单调下降,因此该算法也称为Nesterov ripples。
该算法在固定步长的情况下,收敛条件满足:
\[f(x^{(k)}) - f^{\ast} \leq \frac{2\parallel x^{(0)} - x^{\ast} \parallel_2^2}{t(k+1)^2}\]由此可以看出,Nesterov加速算法收敛速度为\(O(1/\sqrt{\epsilon})\)。当然,我们仍然可以采用backtracking方法实现步长的自动更新,即判断每次更新是否满足下式:\(g(x^+) > g(v) - \nabla g(v)^T (x^+ - v) + \frac{1}{2t} \parallel x^+ - v \parallel_2^2\)。但是与梯度下降和proximal gradient不同的是,这里每次迭代不从\(t=1\)开始,而是从上一次迭代的最终步长\(t=t_{k-1}\)开始,其收敛速度为:
\[f(x^{(k)}) - f^{\ast} \leq \frac{2\parallel x^{(0)} - x^{\ast} \parallel_2^2}{t_{min}(k+1)^2}\]