1. 正态分布
正态分布在数学和计算机等领域中是一个非常重要的概率分布,记为normal distribution,也称为高斯分布。正态分布出现在许多区域统计:例如,采样分布均值是近似地常态的,即使被采样的样本的原始群体分布并不服从正态分布(中心极限定理)。
若随机变量X服从均值为\(\mu\),标准差为\(\sigma\)的概率分布,记为:
\[X \sim N(\mu,\sigma^2)\]则其概率密度函数为:
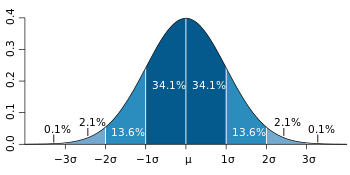
\[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}\]正态分布的概率密度函数曲线呈钟形,对于单变量的正态分布而言,约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。该理论也称为“68-95-99.7法则”或“经验法则”。
2. 正态分布检验
在R中,生成服从正态分布的随机变量序列可通过rnorm()函数实现,服从正态分布的随机变量在某点的pdf和cdf取值分别用dnorm()和pnorm()实现。同时,R中还提供了许多函数用于检验某随机变量是否服从正态分布,如Shapiro-Wilk normality检验、直方图或者QQ图,分别对应R中shapiro.test()、hist()和qqnorm()函数。
其中,Shapiro-Wilk normality test检验也记为SW检验,类似于线性回归的检验方法,是检验其于回归曲线的残差,用于验证一个随机样本数据是否来自正态分布,属于拟合优度统计量检验方法。一般推荐在样本量较小的时候使用该检验方法。SW检验返回两个检验值:p-value和W。当p-value大于显著性水平0.05,不能拒绝零假设:即样本来自正态分布。统计量W 为:
\[W=\frac{(\sum{a_iy_i})^2}{\sum(y_i-\bar{y})^2}\]\(y_i\)是对原随机变量样本排序后得到的样本数据,\(a_i\)可由下式获得:
\[(a_1,\ldots,a_n)=\frac{m^TV^{-1}}{(m^TV^{-1}V^{-1}m)^\frac{1}{2}}\]其中,m是服从标准正态分布的随机变量排序后的期望取值,V是两个排序后变量的协方差矩阵。统计量W最大值是1,可以把W看作是顺序排列样本值\(y_i\)和系数\(a_i\)之间相关系数的平方或者是线性回归的确定性系数,它的值越高,越表示样本与正态分布越匹配。但是仅凭这一个参数是不够的,在非正态分布的小样本数据中也经常会出现较大的W值,所以一般在选用SW检验时,p-value会起到主导作用。
相对SW检验而言,QQ图是将数据的分布与标准正态分布进行比较,属于图示法。如果被比较的两个分布比较相似,则其QQ图近似地位于y = x上。如果两个分布线性相关,则QQ图上的点近似地落在一条直线上,但并不一定是y = x这条线。若样本数据近似正态分布,QQ图上的点会近似的在直线\(Y=\sigma*X+\mu\)附近,其中\(\sigma\)是标准差,\(\mu\)是均值,所以可以通过直线来近似求得所服从的正态分布的参数。
R中的正态分布检验代码如下所示:
#生成服从标准正态分布的随机变量x,样本数为1000 x <- rnorm(1000, mean = 0, sd = 1) #SW检验:样本数量需控制在3~5000 shapiro.test(x) par(mfrow=c(2,2)) #绘制QQ图和直方图 qqnorm(x) hist(x) #随机生成长度为100的服从均匀分布的随机变量 y <- runif(100, min = 0, max = 1) #SW检验 shapiro.test(y) #绘制QQ图和直方图 qqnorm(y) hist(y) dev.off()
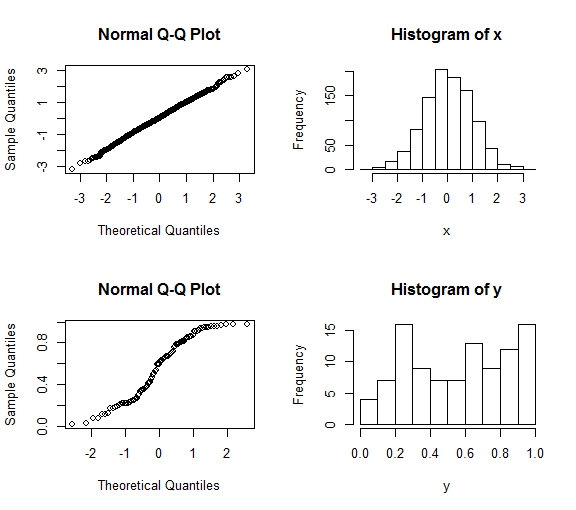
图中第一列为生成服从标准正态分布的随机变量x,第二列对应生成服从均匀分布的随机变量y。通过SW检验结果可以看出随机变量x的p-value大于0.05,不能拒绝原假设,所以随机变量x服从正态分布;相反,随机变量y则明显不服从正态分布。同样,在QQ图中,随机变量x更接近于y=x直线,随机变量y则没有。
3. 多元正态分布
多变量正态分布亦称为多变量高斯分布,它是单维正态分布向多维的推广。该分布可以由以下的PDF来描述,其中\(\sigma\)为变量间的协方差矩阵:
\[f_X(x_1,\ldots,x_N)=\frac{1}{(2\pi)^{\frac{N}{2}}(\mid\sum\mid)^\frac{1}{2}}e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}\]多元正态分布采用svd等矩阵分解方法生成(在SVD算法介绍中讲解该部分内容)。 假设要生成生成序列长度为n,服从d元正态分布的随机变量\(x\sim N_d(\mu,\sum)\),则基本步骤如下:
- 生成大小为n*d维度的矩阵Z,其中Z包含d个长度为n服从标准正态分布的随机变量;
- 计算协方差矩阵的矩阵分解\(\sum=Q^TQ\);
- 使用矩阵的线性变换方法\(X=ZQ+J\mu^T\),其中J为单位列向量;
- 最后获得随机变量X,随机变量X的每行是一个随机变量。