重采样是统计学里的一种采样技术,其适用的情况是待研究的数据是未知概率分布的,因此我们不能得到具体分布的概率密度估计或者累积分布函数。如果已知总体的概率密度函数,我们可以采用点估计和最大似然估计等参数估计方法来计算总体分布的均值或者方差等统计量。在未知统计分布情况下,如果要估计如总体或样本的期望,方差等统计量时,我们需要采用非参数估计方法,如重采样技术。
重采样的核心思想是对数据量较小的样本集每次进行局部采样,得到一个子集,在子集上进行相应的计算,然后多次迭代采样,将结果平均。现在常用的重采样技术有自助法(bootstrap)和刀切法(jackknife)。至于为什么重采样技术可以用于估计样本统计量,我们将会在bootstrap法中重点介绍。
自助法
Bootstrap方法是非参数Monte Carlo方法,其通过重采样对总体分布进行估计。重采样是将观测到的样本视为一个有限总体,从中进行随机再抽样来估计总体的特征以及对抽样总体做出统计推断。
Bootstrap可以是参数Bootstrap或者是非参数Bootstrap。参数Bootstrap是指总体分布已知,利用蒙特卡洛法从此总体中抽样进行统计推断;而非参数Bootstrap是指总体分布完全未知,利用重采样技术从样本中再抽样进行统计推断。这里我们主要介绍非参数估计的Bootstrap方法。对于Bootstrap方法,有限的样本是从总体分布抽样获得,其表示为一个和真实总体具有类似分布特性的“伪总体”。通过从该“伪总体”中重复抽样,然后估计抽样分布的统计量。
重采样或者说Bootstrap方法类似于密度估计,即我们可以通过样本的直方图来估计密度函数的形状。直方图不是密度,但在非参数问题中,它可以被视为是密度的合理估计。之前提到过基于已知概率密度产生随机样本,这里Bootstrap则根据经验分布产生随机样本。
假设\(x=\{x_1,\ldots,x_n\}\)为从总计分布\(F(x)\)中观测得到的样本,\(X^*\)为从x中随机选择的一个样本,则从x中有放回抽样得到随机样本\(X_1^*,\ldots, X_n^*\),则随机变量\(X^*\)服从\(\{x_1,\ldots,x_n\}\)上的均匀分布。此时,随机变量\(X^*\)的分布函数为\(F_n(x)\)可以称为经验分布函数(ecdf)。大数定理告诉我们,无论总体的分布形式\(F(x)\)是否服从高斯分布,如果从随机变量x中抽取n个\(i.i.d.\)样本,那么当n趋向无穷大时,可以有样本均值近似等于总体均值,即 \(E(F(x))=\frac{1}{n}\sum{x_i}\)。
所以有了大数定理作为保证,如果n足够大,那么\(F_n(x)\)对统计量的估计可以逼近与\(F(x)\)的真实值,即对于随机变量x中的任意一个样本\(x_i\)我们可以看成是由随机变量\(X^*\)的分布函数\(F_n(x)\)产生的。所以我们最关键的步骤就是如何估计\(F_n(x)\)。假设我们可以获得m个\(F_n(x)\)产生的样本,当m趋于无限大时,根据大数定理该抽样重复下的经验分布函数\(F_n^*\)是\(F_n\)的逼近。所以根据这个问题我们核心关键步骤就转变为获得m趋于无穷的bootstrap样本。从\(F_n\)中产生随机样本即产生m个服从\(F_n(x)\)的\(i.i.d.\)样本,而\(F_n(x)\)服从于\(\{x_1,\ldots,x_n\}\)的均匀分布,那么该问题就等价于从随机变量x中再抽样m次,即保证Bootstrap抽样过程中是有放回抽样(因为是均匀分布)。那么对x抽采样j轮,每轮做有放回抽样n次\((j*n=m)\),此时,抽取迭代数越大,即j越大,则m越大,根据大数定理的含义,对于总体的统计量估计就会越准确。以上就是重采样或者是bootstrap可以用于估计总体统计量的原因和解释。但是需要注意的是,如果\(F_n(x)\)没有逼近\(F(x)\),则重复抽样下的分布也不会靠近\(F(x)\)。因为无论重复再抽样多少次,得到的Bootstrap样本都没有包含不在在已抽样样本但隶属于总体中的个体。
接下来,我们可以给出Bootstrap的具体实现步骤,如下:
- 对Bootstrap重复抽样的第b次\((b=1,\ldots,B)\):
- 通过有放回的从\(\{x_1,\ldots,x_n\}\)中抽样得到再重采样样本\(x^{*(b)}=x_1^*,\ldots,x_n^*\);
- 根据\(x^{*b}\)计算\(\hat{\theta}^{(b)}\);
- \(F_\hat{\theta}(\cdot)\)的Bootstrap估计为\(\hat{\theta}^{(1)},\ldots,\hat{\theta}^{(B)}\)的经验分布函数。
在R中,对于抽样问题可以采用sample()函数实现,而如果想要实现一个估计量的偏差的Bootstrap估计(Bootstrap估计与样本估计的偏差),即\(bias(\hat{\theta})=E\hat{\theta}-\theta\),可通过使用当前样本下的估计量\(\hat{\theta}\)来估计\(\theta\),而使用\(\hat{\theta}\)的Bootstrap来估计\(E\hat{\theta}\)。如果结果为正偏差,则意味着\(\hat{\theta}\)平均来看过高估计了\(\theta\)。因此我们可以通过偏差修正来重新修正估计量\(\hat{\theta}\)。R中可通过如下代码实现估计量偏差的Bootstrap估计(实验数据源采用Bootstrap包中的法律院校law数据集计算入学平均成绩LSAT和GPA的相关性):
#安装bootstrap包
install.packages("bootstrap")
library(bootstrap) #加载law数据
#计算LSAT和GPA的相关性
theta.hat <- cor(law$LSAT, law$GPA) #计算样本的LSAT和GPA的相关性
B <- 2000 #Bootstrap重采样次数
n <- nrow(law) #sample size
theta.b <- numeric(B) #storage for replicates
#估计量偏差的Bootstrap估计
#bootstrap estimate of standard error of R
for (b in 1:B) {
#randomly select the indices
i <- sample(1:n, size = n, replace = TRUE)
LSAT <- law$LSAT[i] #i is a vector of indices
GPA <- law$GPA[i]
theta.b[b] <- cor(LSAT, GPA)
}
#输出
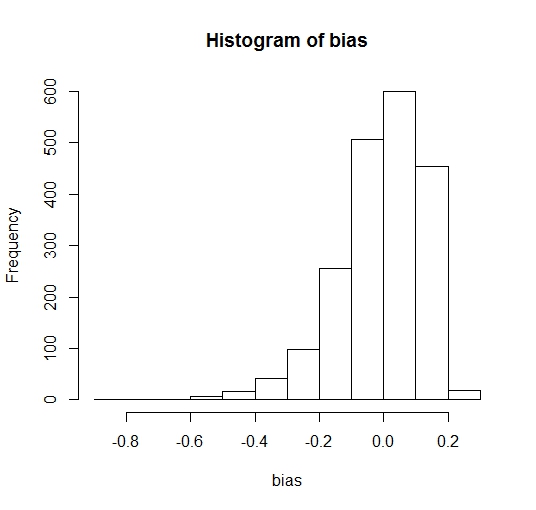
hist(theta.b, prob = TRUE)
print(mean(theta.b))
bias <- theta.b - theta.hat
hist(bias)
m_bias <- mean(theta.b - theta.hat)
print(m_bias)

自助法的置信区间
标准正态Bootstrap置信区间的计算比较简单,假设\(\hat{\theta}\)是参数\(\theta\)的估计量,估计量的标准差为\(se(\hat{\theta})\)。若\(\hat{\theta}\)渐进到正态分布,即\(Z=\frac{\hat{\theta}-E\hat{\theta}}{se(\hat{\theta})}\)渐进服从标准正态分布。这时,若\(\hat{\theta}\)为\(\theta\)的无偏估计,那么\(\theta\)的标准正态Bootstrap置信区间为
\[\hat{\theta}\pm z_{\alpha/2}\hat{se}_B(\hat{\theta})\]其中,\(z_{\alpha/2}=\phi^{-1}(1-\alpha/2)\)。
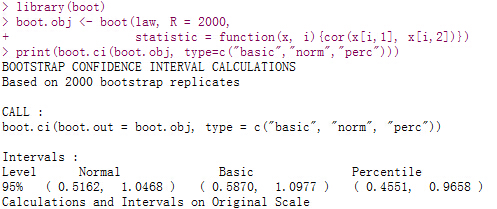
当然,标准Bootstrap置信区间估计要满足正态性和无偏性等条件,且即使\(se(\hat{\theta})\)为正态分布,统计量\(Z\)的分布也不一定是正态的。这时可采用Bootstrap百分位数置信区间和Bootstrap t置信区间解决该问题。在R中可采用boot包的boot.ci()函数实现Bootstrap置信区间的计算。例如计算law数据Bootstrap估计的置信区间,代码如下所示,三种置信区间都覆盖了相关系数0.769(上面介绍的关于Bootstrap计算law数据集中平均成绩LSAT和GPA的相关性的例子)。
library(boot)
data(law, package = "bootstrap")
boot.obj <- boot(law, R = 2000,
statistic = function(x, i){cor(x[i,1], x[i,2])})
print(boot.ci(boot.obj, type=c("basic","norm","perc")))
刀切法
刀切法(Jackknife)是由Quenouille于1949年提出的重采样方法,比bootstrap早几十年,Jackknife类似于“leave-one-out”的交叉验证方法。刀切法基本步骤是:每次从样本集中删除一个样本,剩余的样本成为“刀切”样本,由一组这样的刀切样本计算统计量的估计值。
总体来说刀切法是基于点估计的无偏准则,这里再简单复述点估计的相关概念:点估计是用抽样样本的观察值所计算获得的估计值\(\hat{\theta}\)作为总体的未知参数\(\theta\)的估计量,而无偏性是指点估计的估计量\(E\hat{\theta}=\theta\),无偏性意味着只有在大量重复抽样时才会获得与真值偏差不大的估计量。所以刀切法只适用于光滑参数统计量的估计:光滑意味着样本的微小改变只会引起估计量\(\theta\)的微小变化(如:均值为平滑参数,而中位数则为非平滑参数)。对于非光滑参数的估计,刀切法去掉一个或者多个样本使得统计量的估计变化幅度非常大,不能在真实值附近波动,就不能很好的服从于点估计的无偏一致性。
对于光滑的参数估计,刀切法的原始动机是降低估计的偏差,因为如果参数是光滑的,那么对参数的多次估计必然服从无偏准则,这样能大幅度减小一次估计带来的偏差。同时,通过对统计量的多次估计,不但可以减少算法的偏差,还可以得到算法的稳定性衡量(方差)。但需要指出的是缩小偏差并不是一个好的办法,因为无偏估计只适用于线性统计量的方差估计,对于非线性统计量方差估计的偏差趋近于0,其均方误差会变得很大,导致过拟合,误差平方和仍然很大。
这里假设我们要估计的统计量为光滑的,令\(x=(x_1,\ldots,x_n)\)为观测到的样本,定义第\(i\)个Jackknife样本为丢掉第\(i\)个样本后的剩余样本,即\(x_{(i)}=(x_1,\ldots,x_{i-1},x_{i+1},\ldots,x_n)\)。若\(\hat{\theta}=T_n(x)\),则定义第\(i\)次Jackknife抽样估计为\(\hat{\theta}_{(i)}=T_{n-1}(x_{i}),i=1,\ldots,n\)。
在自助法中我们介绍了估计量偏差的Bootstrap估计,这些估计本身又是估计量,对于这些估计量的方差估计就可以使用Jackknife方法来估计这些估计量的方差。这种方法也成为Jackknife-after-Bootstrap方法,这里就不在过多介绍该方法了。
联系与区别
Efron在1979年发表的文章指出了自助法与刀切法的关系:
-
自助法通过经验分布函数将不确定的估计概率分布的问题转化为从给定样本集中重采样;
-
自助法可以解决不光滑参数的问题。遇到不光滑(Smooth)参数估计时,刀切法会失效;
-
将自助法估计用泰勒公式展开,可以得到刀切法是自助法方法的一阶近似;
-
对于线性统计量的估计方差这个问题,刀切法或者自助法会得到同样的结果。但在非线性统计量的方差估计问题上,刀切法严重依赖于统计量线性的拟合程度,所以远不如自助法有效;
这里,我们以对于一个不平滑参数(中位数)的统计量的 估计为例来说明刀切法在非平滑统计量估计中失效的问题,例如估计从1,2,…,100中随机抽取10个数的中位数的标准差:
#刀切法与自助法
#设定种子数,保证每次产生的随机数一致
set.seed(1)
#设定从1~100中随机抽取10个数
n <- 20
x <- sample(1:100, size = n)
z <- 1:100
#刀切法估计量的标准差
M <- numeric(n)
for (i in 1:n) {
y <- x[-i]
M[i] <- median(y)
}
Mbar <- mean(M)
#自助法估计量的标准差
Mb <- replicate(1000, expr = {
y <- sample(x, size = n, replace = TRUE)
median(y) })
#输出
#抽样获得的10个样本
print(x)
#刀切法对中位数的估计值
print(M)
#自助法对中位数的估计值
print(head(Mb))
#总体z的中位数
sprintf("总体z的中位数为%g,标准差为%g",
median(z),sqrt(sum(x-median(z))^2/n))
#随机变量x的中位数
sprintf("随机变量x的中位数为%g,标准差为%g",
median(x),sqrt(sum(x-median(x))^2/n))
##输出刀切法的对中位数估计的标准差
sprintf("刀切法估计的中位数为%g,标准差为%g",
Mbar, sqrt((n-1)/n * sum((M - Mbar)^2)))
##输出自助法的对中位数估计的标准差
sprintf("自助法估计的中位数为%g,标准差为%g",mean(Mb),sd(Mb))

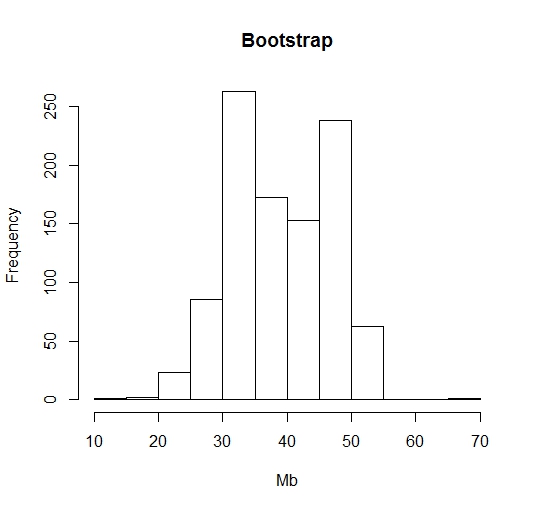
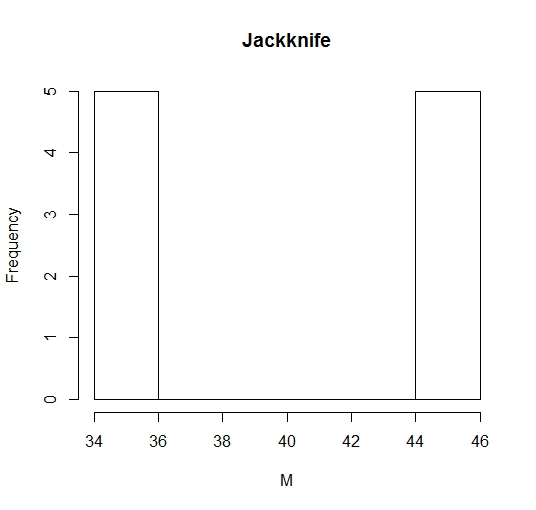
从结果可以看出,对于中位数的标准差的估计很大,与Bootstap估计值相差很远。这是因为中位数是不平滑的,所以对于不平滑参数的估计刀切法是失效的,它在中位数估计中只会出现35和45两种数值,方差较大,而bootstrap方法则对中位数估计的方差较小,如下各方法估计量的直方图。如果将非光滑参数改为光滑参数,如均值,则刀切法和自助法对从1,2,…,100中随机抽取10个数的均值的标准差估计分别为6.494和6.182,很接近,说明对于光滑参数而言,这两种重采样方法的估计量基本一致。