核密度估计
1. NDE
对于直方图密度估计,如果随机变量为\(X_1, \ldots, X_n\),直方图的带宽为\(h\),则点\(x\)附近的密度估计为:
\[\hat{f}(x)=\frac{1}{2hn}\times k\]此时,k为落在区间\((x-h, x+h)\)内样本点的个数。而本文所要讲述的核密度估计是对直方图密度估计思想的扩展,我们可以把上式写为:
\[\hat{f}(x)=\frac{1}{n}\sum_{i=1}^{n}\frac{1}{h}w(\frac{x-X_i}{h})\]其中,令\(w(\frac{x-X_i}{h})=w(t)= \frac{1}{2}I(\|t\|<1)\)是权值函数,也称为朴素密度估计(naive density estimator)。因为\(w(t)\)是权值函数,所以具有以下性质:\(\int_{-1}^1w(t)dt=1\)和\(w(t)\geq0\)。
2. KDE
核密度估计(kernel density estimation)是采用核函数\(K(\cdot)\)代替NDE中权值函数,用于估计概率密度的方法。同样,核函数服从\(\int_{-\infty}^{\infty}K(t)dt=1\)。一般而言,核函数是对称函数,例如,上述\(w(t)=\frac{1}{2}I(\|t\|<1)\)称为矩形核函数(或矩形窗函数),原点为矩形窗的中心;前面所提到的\(\frac{1}{nh}w(\frac{x-X_i}{h})\)即是以\(X_i\)为中心,以\(\frac{1}{n}\)为面积的矩形窗,而在点\(x\)的密度估计即\(\hat{f}(x)\)等于在距\(x\)点\(h\)单位内矩形面积总和。所以核密度估计一般表达式可根据上述朴素密度估计写为:
\[\hat{f}_K(x)=\frac{1}{n}\sum_{i=1}^{n}\frac{1}{h}K(\frac{x-X_i}{h})\]\(\hat{f}_K(x)\)为概率密度函数,且其具有和\(K(x)\)一样的连续性和差分性,即如果\(K(x)\)为概率密度核函数,则\(\hat{f}_K(x)\)为连续函数;如果\(K(x)\)存在r阶微分\(K^{(r)}(x)\),则\(\hat{f}_K(x)\)也存在r阶差分。\(h\)一般记为核函数的带宽,也称为光滑参数、窗长。例如,上节讲的直方图密度估计属于矩形核密度估计,\(h\)越小,容易欠光滑,过度反应局部信息;\(h\)越大,易过光滑,丢失样本信息。
3. 高斯核函数
高斯核函数(Gaussian Kernel Function)是最为常用的核函数之一,\(K(G)=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}(\frac{x-\mu}{\sigma})^2)\)。高斯核函数的性质在概率密度函数中做过介绍,这里主要介绍如何选取高斯核函数的最优带宽\(h_{optimal}\)。在《概率密度估计》一讲中,我们介绍过三种光滑参数的优化方法:Sturges、Scott和Freedman-Diaconis规则。在R中,高斯核密度估计的最优带宽选择默认的优化方法是Scott规则。
Struges规则是采用离散二项分布逼近正态分布获得正态分布的参数,而Scott规则则是利用优化方法中的\(L_2\)准则,以减少估计的均方误差为目标,并将其作为带宽选择的代价函数进行优化。
对于密度估计而言,在点\(x\)上的估计\(\hat{f}(x)\)的均方误差(MSE)为:
\[MSE(\hat{f}(x))=E(\hat{f}(x)-f(x))^2=Var(\hat{f}(x))+bias^2(\hat{f}(x))\]MSE是对样本点逐点的衡量估计误差,而误差积分准则中的平误差积分准则(integrated squared error)ISE是对\(\hat{f}\)整个支撑域上\(f\)的估计量:
所以,均方误差积分(mean integrated squared error)MISE为:
Scott规则根据MISE定义,利用泰勒级数展开,设定高斯核函数密度估计中光滑参数的代价函数为:
\[MISE=\frac{\int f(x)^2dx}{nh}+\frac{h^4\sigma^4\int f^{,,}(x)^2dx}{4}+O(\frac{1}{nh}+h^4)\]此时,通过优化代价函数,最优带宽等于:
\[h_n^*=(\frac{\int f(x)^2dx}{n\sigma^4\int f^{,,}(x)^2dx})^{1/5}\]Scott准则(Scott’s Normal Reference Rule)将上式\(h_n^*\)校准到标准差为\(\sigma^2\)的正态分布,最优带宽可变为:
\[h_n^*={4/3}^{1/5}\sigma n^{-1/5}\doteq1.06\hat{\sigma}n^{-1/5}\]其中,\(\hat{\sigma}\)为抽样样本的方差,用于代表总体方差。
但是,该带宽参数优化方法只适用于样本分布属于正态分布,如果样本分布是有偏分布,该方法会使得估计带宽过光滑。因此,Silverman提出一种更为健壮的估计方法,该方法设定\(\hat{\sigma}=min(S,IQR/1.34)\),其中\(S\)为样本标准差,\(IQR\)是样本的四分点。最优带宽为:
\[h_n^*=0.9\hat{\sigma}n^{-1/5}=0.9min(S,IQR/1.34)n^{-1/5}\]4. 实例
R中,密度估计通过density()函数实现,其中R默认选用的核函数为高斯核函数(共提供7种核函数:gaussian,epanechnikov,rectangular,triangular,biweight,cosine和optcosine),光滑参数为bw。
本实例通过R代码实现对Old Faithful数据中waiting time特征的密度估计。Old Faithful数据采集自美国黄石公园内的一个名叫Old Faithful 的喷泉。“waiting”就是喷泉两次喷发的间隔时间,“duration”当然就是指每次喷发的持续时间。高斯核密度估计的R代码如下:
library(MASS)
waiting <- geyser$waiting
n <- length(waiting)
#Scott方法
h1 <- 1.06*sd(waiting)*n^(-1/5)
#Silverman方法
h2 <- 0.9*min(c(sd(waiting), IQR(waiting)/1.34))*n^(-1/5)
#默认方法
par(mfrow=c(2,2))
hist(waiting, freq=FALSE, xlab="default", main="hist: default")
plot(density(waiting))
plot(density(waiting,h1))
plot(density(waiting,h2))
#最优带宽计算结果对比
sdK <- density(waiting)
print(sprintf("R中density带宽默认方法、Scott方法和Silverman方法
计算结果分别为:%g, %g, %g",sdK$bw, h1, h2))

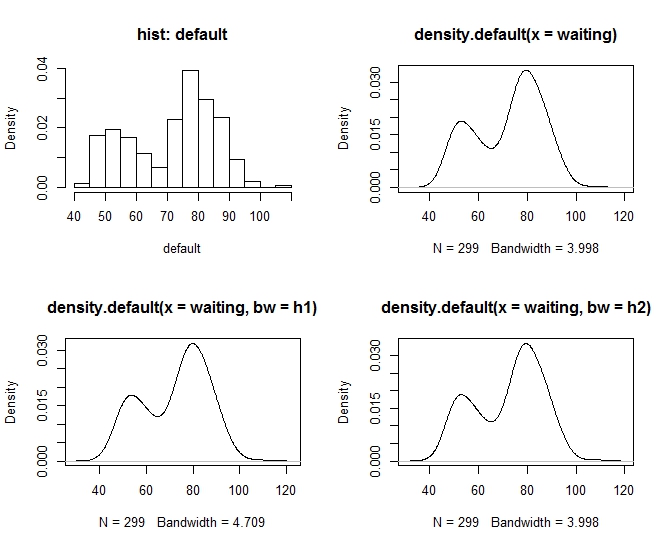
实验结果证明,R中默认带宽计算方法是改进的Silverman法,最优带宽为3.998;而Scott法结果与默认方法接近,最优带宽为4.708。总体来说,Silverman法不要求样本必须服从正态分布或者核函数是对称的,具有更广泛的适用性。