1. 参数估计与非参数估计
在研究随机变量的过程中,随机变量的概率密度函数的作用是描述随机变量的特性;在分类器设计过程中,需要在类的先验概率和类条件概率密度函数已知下,确定判别函数。但是在实际应用中,总体概率密度函数通常是未知的,那么如何来估计总体概率密度呢?一般,我们通过抽样或者采集一定的样本,可以根据统计学知识从样本集合中推断总体概率密度。这种方法统称为概率密度估计,即根据训练样本来确定随机变量的概率分布。一般概率密度估计方法方法大致分为两类:参数估计和非参数估计。
参数估计(Parametric Estimation)是根据对问题的经验知识,假设随机变量服从某种分布,即假定概率密度函数的形式,然后通过训练数据估计出分布函数的参数。常见的参数估计方法有最大似然方法和贝叶斯方法。对于参数估计,根据样本中是否已知样本所述类别将参数估计又划分为监督参数估计和非监督参数估计。
非参数估计(Nonparametric Estimation)则是在不假定总体分布形式下, 基于大样本的性质,直接利用样本估计出整个函数。在很多情况下,我们对样本的分布并没有充分的了解,无法事先给出密度函数的形式,而且有些样本分布的情况也很难用简单的函数来描述。在这种情况下,就需要用到非参数估计。但是,并不是非参数估计一定优于参数估计,因为非参数估计受训练样本影响,其完备性或者说是泛化能力不会很好;且这种估计只能用数值方法取得,无法得到完美的封闭函数图形。常用的非参数估计方法有直方图法,核概率密度估计等。
本文主要针对非参数估计的直方图法进行介绍。
2. 直方图密度估计
直方图(Histogram)是什么我想就不过多介绍了,对于概率密度估计而言,直方图方法是对概率密度的分段连续估计方法,影响估计的关键因素是直方图的箱的个数,即箱子的带宽。对于训练数据而言,该参数作为一个平滑参数,决定着估计结果的光滑程度。一般而言,训练数据中都含有噪声,如果箱子带宽设定过小,则会出现欠光滑,展示过多训练集的细节;如果带宽过大,则会过光滑,屏蔽训练集可能存在的重要特征。
假设观测到的随机变量为\(X_1,\ldots,X_n\),如果构建针对随机变量\(X\)的直方图,首先需要对观测数据进行排序,放进对应的箱中。装箱过程由平滑参数(箱子带宽)决定,理论上箱子的带宽可以为任意值,但为获得合理的总体概率密度信息,则需要一定规则或者方法用于选取箱子带宽。目前有Sturges、Scott和Freedman-Diaconis规则等方法用于解决如何选取箱子带宽。
给定箱子的带宽\(h\),直方图密度估计为\(\hat{f}(x)=\frac{v_k}{nh}, t_k \leq x < t_{k+1}\),其中\(n\)为随机变量样本总量,\(v_k\)为落在\([t_k,t_{k+1})\)区间内的样本数量。如果箱子带宽\(h=1\)时,则直方图概率密度估计则等同于样本点的频率。有了直方图概率密度估计的一般形式,我们接下来介绍上述三种平滑参数估计方法中的一种:Sturges‘ Rule。
Sturges’ Rule
Sturges’ Rule方法是R包中hist()函数默认选取箱子带宽的方法,但该方法容易使得直方图过光滑。Sturges’ Rule方法是基于抽样样本属于正态分布假设下,当样本量足够大趋于无限时,采用离散分布函数中的二项分布(其中\(p=0.5\))逼近正态分布,最终获得正态分布的均值和标准差。
例如,假设随机变量\(X_1,\ldots,X_n\)的样本量\(n=64\),对于二项分布\(Binomial(k,1/2)\)而言,\(k=\log_2n=\log_{2}64=6\)。所以二项分布\(Binomial(6,1/2)\)各类别(例如完成64次连续抛硬币6次的试验中出现正面的次数)的频率为
\[({6 \atop 0}),({6 \atop 1}),({6 \atop 2}),\ldots,({6 \atop 6})=1,6,15,20,15,6,1\]所以,当k趋近于无穷,即样本量n无限大时,二项分布\(Binomial(k,1/2)\)收敛于正态分布\(Normal(\mu=n/2,\sigma^2=n/4)\)。这证明了,当n足够大时,正态分布可由二项分布表示,也就意味着连续概率密度函数可由离散分布函数所表示。
此时,对于直方图概率密度估计而言,箱子的个数为\(k+1=7\)个,每个箱子的带宽则为\(\frac{R}{1+\log_2n}=\frac{7}{1+\log_{2}64}=1\),其中R为样本的值域(变化范围),这里以抛硬币的多重贝努力实验为例,R代表连续抛6次硬币出现正面可能性的个数,故R=7。由于我们仅讨论箱子带宽固定的情况,所以箱子个数和带宽对于R成反比关系。
综上所述,Sturges’ Rule方法定义在一定样本量下,最优箱子带宽长度为:
\[\frac{R}{1+\log_2n}\]但需要注意的是,箱子的带宽或者箱子的个数仅由样本量n决定,与抽样样本的概率密度分布无关。所以,Sturges’ Rule方法适用于总体样本服从对称、单峰的分布形式,不适用于倾斜或者多峰的分布。
3. 实例
对于标准正态分布,样本量为25情况下,直方图概率密度估计(hist())的默认方法和Struges’ Rule方法的R代码如下:
n <- 25
x <- rnorm(n)
#根据Sturges' Rule方法计算带宽
nclass <- ceiling(1+log2(n))
cwidth <- diff(range(x) / nclass)
breaks <- min(x) + cwidth * 0:nclass
#产生1000个标准正态分布的随机数
z <- qnorm(ppoints(1000))
#绘制默认hist函数的直方图
h.default <- hist(x, freq=FALSE, xlab="default", main="hist: default")
lines(z, dnorm(z))
#绘制Sturges' Rule方法的直方图
h.sturges <- hist(x, breaks=breaks, freq=FALSE, main="hist: sturges")
lines(z,dnorm(z))
#默认方法的分界点
print(h.default$breaks)
#默认方法的落入箱子的点的个数
print(h.default$counts)
#Sturges' Rule方法的分界点
print(round(h.sturges$breaks, 1))
#Sturges' Rule方法的落入箱子的点的个数
print(h.sturges$counts)
#两种方法绘制直方图的箱子的带宽
print(sprintf("默认方法和Sturges方法对应绘制直方图的箱子带宽为%g, 和%g",
h.default$breaks[2]-h.default$breaks[1], cwidth))
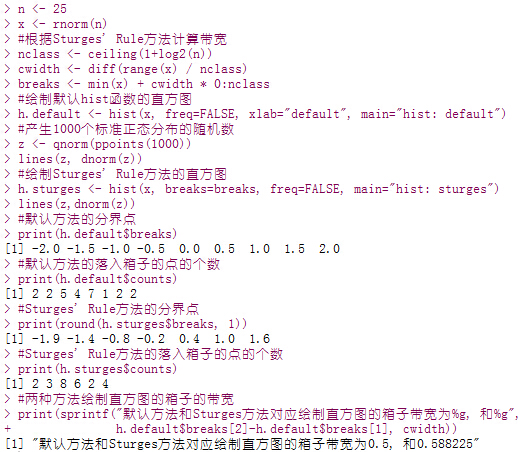
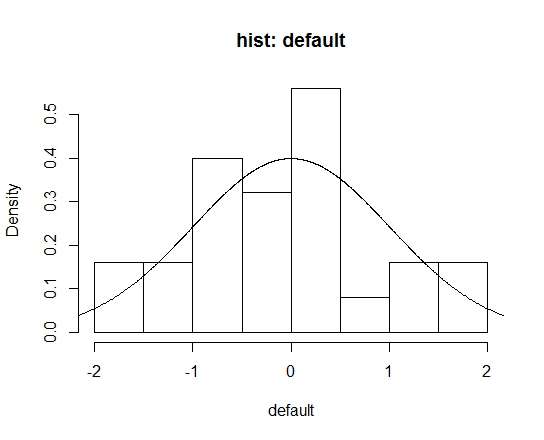
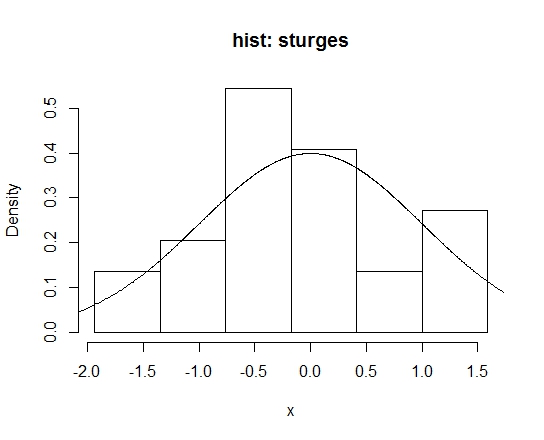
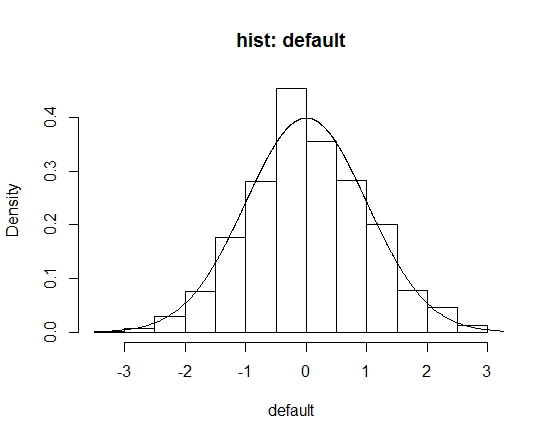
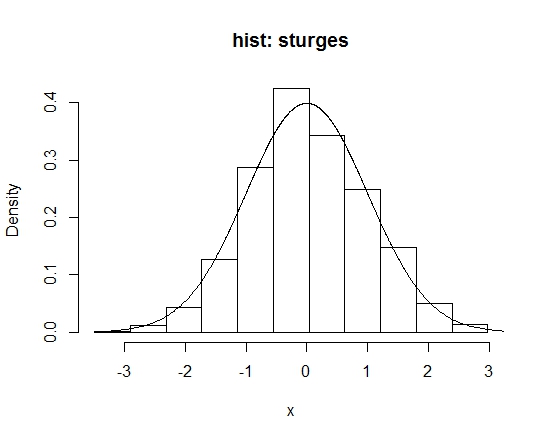
这里需要指出的是,Struges方法虽然是hist函数break参数中的默认选项,但仅作为建议,其真正默认划分方式是根据pretty()函数计算得到的。如果没有给出break参数,则Struges方法不会被调用。所以,从结果中可以看出,默认hist函数的结果与调用Struges结果不太一样,二者箱子带宽分别为0.5和0.588。当样本量足够大时,默认方式与Struges结果基本一致,如下图所示(\(n=1000\)):