1. 次梯度
在优化问题中,我们可以对目标函数为凸函数的优化问题采用梯度下降法求解,但是在实际情况中,目标函数并不一定光滑、或者处处可微,这时就需要用到次梯度下降算法。
次梯度(*Subgradient*)与梯度的概念类似,凸函数的First-order characterization是指如果函数f可微,那么当且仅当\(dom(f)\)为凸集,且对于\(\forall x,y \in dom(f)\),使得\(f(y) \geq f(x)+\nabla f(x)^T(y−x)\),则函数\(f\)为凸函数。这里所说的次梯度是指在函数\(f\)上的点\(x\)满足以下条件的\(g \in \mathbb{R}^n\):
其中,函数\(f\)不一定要是凸函数,非凸函数也可以,即对于凸函数或者非凸函数而言,满足上述条件的\(g\)均为函数在该点的次梯度。但是,凸函数总是存在次梯度(可以利用epigraph和支撑平面理论证明),而非凸函数则不一定存在次梯度,即使\(f\)可微。该定义说明,用次梯度对原函数做出的一阶展开估计总是比真实值要小。
很明显,凸函数的次梯度一定存在,如果函数\(f\)在点\(x\)处可微,那么\(g=\nabla f(x)\),为函数在该点的梯度,且唯一;如果不可微,则次梯度不一定唯一。但是对于非凸函数,次梯度则不一定存在,也不一定唯一。例如,凸函数\(\parallel x \parallel_p\)范数为凸函数,但不满足处处可微的条件,因此,函数的次梯度不一定唯一,如下图:
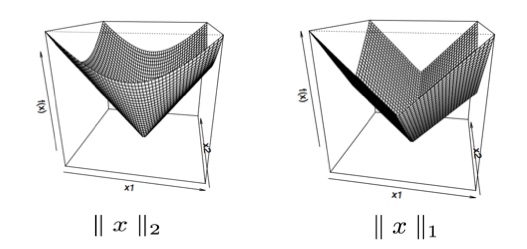
左一图为\(\parallel x \parallel_2\),函数在\(x \neq 0\)时,次梯度唯一,且\(g=x / \parallel x \parallel_2\);当\(x = 0\)时,次梯度为\(\{ z: \parallel z \parallel_2 \leq 1 \}\)中的任意一个元素;
左二图为\(\parallel x \parallel_1\),函数在\(x \neq 0\)时,次梯度唯一,且\(g=sign(x)\);当\(x = 0\)时,次梯度为\([-1,1]\)中的任意一个元素;
同样,绝对值函数\(f(x)=\mid x\mid\)和最大值函数\(f(x)=max\{ f_1(x), f_2(x) \}\)在不可微点处次梯度也不一定唯一,如下图:
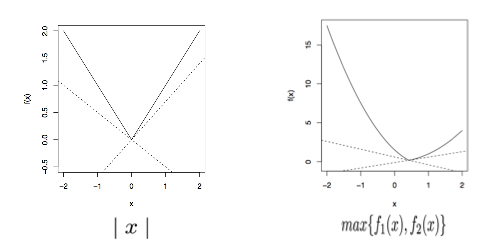
对于左二函数而言,其在满足\(f_1(x)=f_2(x)\)的点处,次梯度为任意一条直线在向量\(\nabla f_1(x)\)和\(\nabla f_2(x)\)之间。
同理,我们还可以给出次微分(subdifferential)的定义,即:
\[\partial f(x) = \{ g \in \mathbb{R}^n: g \, is \, a \, subgradient \, of \, f \, at \, x \}\]-
次微分是闭合且为凸集;
-
如果函数\(f\)在点\(x\)处可微,那么次微分等于梯度;
-
凸函数的次微分不为空,但非凸函数则不一定。
如果我们还记得Normal cone是指给定任意集合\(C\)和点\(x \in C,\mathbb{N}_C(x)={g:g^Tx \geq g^Ty}\),那么我们可以看出,对于集合\(C\)的边界上点的Normal cone就是函数\(I_C(x)\)在该点的次微分。其中,
\begin{equation}
I_C(x)=I{ x \in C }=
\begin{cases}
0 \quad & if \, x \in C\
\infty \quad & if \, x \notin C
\end{cases}
\end{equation}
证明:
因为,对于函数的次梯度会满足\(I_C(y) geq I_C(x) + g^T(y-x)\),因此,
-
对于\(y \notin C\),\(I_C(y)=\infty\),不满足Normal cone的定义;
-
对于\(y \in C\),\(0 \geq g^T(y-x)\),满足Normal cone的定义;
既证。
2. 次梯度的性质
-
Scalingf:\(\partial (af)=a\cdot \partial f\);
-
Addition:\(\partial (f_1+f_2)=\partial f_1 + \partial f_2\);
-
Affine composition:如果\(g(x)=f(Ax+b)\),那么\(\partial g(x)=A^T \partial f(Ax+b)\);
-
Finite pointwise maximum:如果\(f(x)=\max \limits_{i=1,\ldots,m} f_i(x)\),那么\(\partial f(x)=conv(\bigcup \limits_{i:f_i(x)=f(x)} \partial f_i(x))\),意味着函数\(f(x)\)的次微分等于所有能取得最大值的函数\(f_i(x)\)在点\(x\)处的微分,具体实例可参考之前提到的最大值函数部分。
3. 为什么要计算次梯度?
对于光滑的凸函数而言,我们可以直接采用梯度下降算法求解函数的极值,但是当函数不处处光滑,处处可微的时候,梯度下降就不适合应用了。因此,我们需要计算函数的次梯度。对于次梯度而言,其没有要求函数是否光滑,是否是凸函数,限定条件很少,所以适用范围更广。
次梯度具有以下优化条件(subgradient optimality condition):对于任意函数\(f\)(无论是凸还是非凸),函数在点\(x\)处取得最值等价于:
\[f(x^{\ast})=\min \limits_{x} f(x) \, \Leftrightarrow \, 0 \in \partial f(x^{\ast})\]即,当且仅当0属于函数\(f\)在点\(x^{\ast}\)处次梯度集合的元素时,\(x^{\ast}\)为最优解。
证明:
证明很简单,当次梯度\(g=0\)时,对于所有\(y \in dom(f)\),存在\(f(y) \geq f(x^{\ast}) + 0^T (y-x^{\ast})=f(x^{\ast})\),所以,\(x^{\ast}\)为最优解,即证。
4. 次梯度算法
次梯度算法(Subgradient method)与梯度下降算法类似,仅仅用次梯度代替梯度,即:
\[x^{(k)} = x^{(k-1)} - t_k \cdot g^{(k-1)}, \, k=1,2,3,\ldots\]其中,\(g^{(k-1)} \in \partial f(x^{(k-1)})\),为\(f(x)\)在点\(x\)处的次梯度。
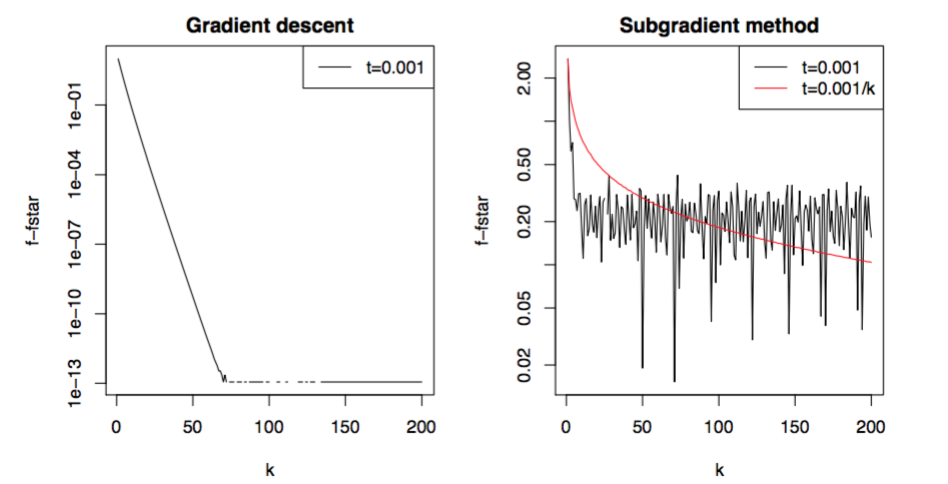
与梯度下降算法不同的地方在于,次梯度算法并不是下降算法,每次对于参数的更新并不能保证代价函数是呈单调递减的趋势,因此,一般请款下我们选择:
\[f(x_{best}^{(k)}) = \min \limits_{i=0,\ldots,k} f(x^{(i)})\]另一点与梯度下降算法不同的是:次梯度算法没有明确的步长选择方法,类似Exact line search和Backtracking line search的方法,只有步长选择准则,具体如下:
Fixed step sizes: \(t_k = t, \, all \, k = 1,2,3,\ldots\);Diminishing step sizes: 选择满足以下条件的\(t_k\):
Diminishing step sizes方法主要是保证步长逐渐变小,同时,变化幅度还不会特别快。这里需要注意的是,次梯度算法并不像梯度下降一样,可以在每一次迭代过程中自适应的计算此次步长(adaptively computed),而是事先设定好的(pre-specified)。
但是,很多人会提出这样一个问题,如果你不能保证次梯度是单调的,如何保证最后可以收敛?
定理:如果\(f\)为凸函数,且满足Lipschitz continuous with G,如果固定步长为\(t\),那么次梯度算法满足:
\[\lim \limits_{k \rightarrow \infty} f(x_{best}^{(k)}) \leq f^{\ast} + \frac{G^2 t}{2}\]证明:
对于\(\forall k\),\(x^{(k+1)} = x^{(k)} - t g^{(k)}\),其中\(g \in \partial f(x)\)。因此,我们可以展开下式为:
\begin{equation}
\begin{split}
\parallel x^{(k+1)} - x^{\ast} \parallel_2^2 & = \parallel x^{(k)} - t g^{(k)} - x^{\ast} \parallel_2^2 \
& = \parallel x^{(k)}-x^{\ast} \parallel_2^2 - 2 t g^{(k)}(x^{(k)} - x^{\ast}) + t^2 \parallel g^{(k)} \parallel_2^2
\end{split}
\end{equation}
因为,\(f(x^{\ast}) = f^{\ast}\),且由凸函数一阶性质可得\(f(x^{\ast}) \geq f(x^{(k)}) + g^{(k)T}(x^{\ast}-x^{(k)})\),上式不等式可以写为:
\[\parallel x^{(k+1)} - x^{\ast} \parallel_2^2 \leq \parallel x^{(k)}-x^{\ast} \parallel_2^2 - 2t (f(x^{(k)}) - f^{\ast}) + t^2 \parallel g^{(k)} \parallel_2^2\]对于任意\(k=1,2,\ldots, K\),求和上式可以获得:
\begin{equation}
\begin{split}
\sum_{k=1}^K (\parallel x^{(k+1)} - x^{\ast} \parallel_2^2 - \parallel x^{(k)} - x^{\ast} \parallel_2^2) & = \parallel x^{(k+1)} - x^{\ast} \parallel_2^2 - \parallel x^{(1)} - x^{\ast} \parallel_2^2 \
& \leq -2t \sum (f(x^{(i)}) - f^{\ast}) + \sum t^2 \parallel g^{(i)} \parallel_2^2
\end{split}
\end{equation}
因为,\(\parallel x^{(k+1)} - x^{\ast} \parallel_2^2 \geq 0\),所以:
\[2t \sum_{i=1}^k (f(x^{(i)}) - f^{\ast}) \leq \parallel x^{(1)} - x^{\ast} \parallel_2^2 + \sum_{i=1}^k t^2 \parallel g^{(i)} \parallel_2^2\]如果令\(f(x_{best}^{k})\)为迭代\(k\)次内的最优解,那么\(f(x_{best}^{(k)}) \leq f(x^{(i)})\),其中,\(i=1,2,\ldots,k\),因此:
\[2tk(f(x_{best}^{(k)}) - f^{\ast}) = 2t \sum_{i=1}^k (f(x_{best}^{(k)}) - f^{\ast}) \leq 2t \sum_{i=1}^k (f(x^{(i)}) - f^{\ast}) \leq \parallel x^{(1)} - x^{\ast} \parallel_2^2 + \sum_{i=1}^k t^2 \parallel g^{(i)} \parallel_2^2\]所以,我们可以得到\(f(x_{best}^{(k)}) - f^{\ast} \leq \frac{\parallel x^{(1)} - x^{\ast} \parallel_2^2 + \sum_{i=1}^k t^2 \parallel g^{(i)} \parallel_2^2}{2tk}\)
同时,因为函数满足Lipschitz continuous with G,所以,\(\mid f(x) - f(y) \mid \leq \parallel x-y \parallel_2\),即函数的次梯度\(\parallel g \parallel_2 \leq G\)。
综上所述,我们可以证明下式成立:
\begin{equation}
\begin{split}
f(x_{best}^{(k)}) - f^{\ast} & \leq \frac{\parallel x^{(1)} - x^{\ast} \parallel_2^2 + t^2 k G^2}{2tk} \
& = \frac{R^2}{2tk}+ \frac{G^2t}{2}
\end{split}
\end{equation}
当\(k \rightarrow \infty\),既证上述定理成立。
此时,如果我们想要获得\(\epsilon\)-最优解,则令\(\frac{R^2}{2tk}+ \frac{G^2t}{2} = \epsilon\),令等式的每一部分等于\(\frac{\epsilon}{2}\),则\(k=\frac{R^2}{t} \cdot \frac{1}{\epsilon}=\frac{R^2G^2}{\epsilon^2}\)。
因此,次梯度的收敛速度为\(O(\frac{1}{\epsilon^2})\),跟梯度下降算法收敛速度\(O(\frac{1}{\epsilon})\)相比,要慢许多。
5. 次梯度算法实例
A. Regularized Logistic Regression
对于逻辑回归的代价函数可记为:
\[f(\beta) = \sum_{i=1}^n (-y_i x_i^T \beta + log (1+exp(x_i^T \beta)))\]明显,上式是光滑且凸的,而regularized problem则是指优化目标函数为:
\[\min \limits_{\beta \in \mathbb{R}^p} f(\beta) + \lambda \cdot P(\beta)\]如果\(P(\beta)=\parallel \beta \parallel_2^2\),则成为岭回归(ridge problem),如果\(P(\beta)=\parallel \beta \parallel_1\)则称为Lasso。对于岭回归,我们仍然可以采用梯度下降算法求解目标函数,因为函数处处可导光滑,而Lasso问题则无法用梯度下降算法求解,因为函数不是处处光滑,具体可参考上面给出的Norm-1的定义,所以,对于Lasso问题需要选用次梯度算法求解。
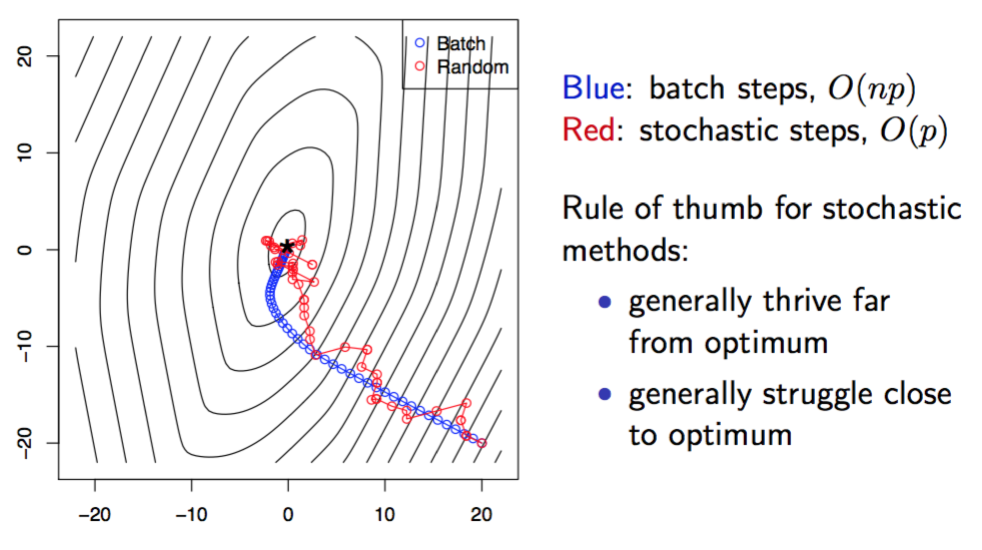
下图是对于同样数据集下分别对逻辑回归选用岭惩罚和Lasso惩罚求解最优解的实验结果图(\(n=1000, p=20\)):
B. 随机次梯度算法
第4部分降到的次梯度算法梯度更新定义为:
\[x^{(k)} = x^{(k-1)} - t_k \cdot \sum_{i=1}^m g_{i}^{(k-1)}, \, k=1,2,3,\ldots\]随机次梯度算法(Stochastic Subgradient Method)与次梯度算法(Subgradient Method)相比,每次更新次梯度是根据某一个样本计算获得,而不是通过所有样本更新次梯度,其定义为:
\[x^{(k)} = x^{(k-1)} - t_k \cdot g_{ik}^{(k-1)}\]其中,\(i_k \in \{1,\ldots,m \}\)是第\(t\)次迭代随机选取的样本\(i\)。从该方法的定义,我们也可引出随机梯度下降算法(Stochastic Gradient Descent)的定义,即当函数\(f\)可微连续时,\(g_i^{(k-1)} = \nabla f_i(x^{(k-1)})\)。
所以,根据梯度更新的方式不同,次梯度算法和梯度下降算法一般被称为“batch method”。从计算量来讲,\(m\)次随机更新近似等于一次batch更新,二者差别在于\(\sum_{i=1}^m[\nabla f_i(x^{(k+i-1)}) - \nabla f_i(x^{(k)})]\),当\(x\)变化不大时,差别可以近似等于0。
对于随机更新次梯度,一般随机的方式有两种:
- Cyclic rule:选择\(i_k = 1,2,\ldots,m,1,2,\ldots,m,\ldots\);
- Randomized rule:均匀随\(\{1,\ldots,m\}\)机从选取一点作为\(i_k\)。
与所有优化算法一样,随机次梯度算法能否收敛?
答案是肯定的,这里就不在做证明,有兴趣的同学可以参考boyd教授的论文,这里仅给出收敛结果,如下:
\[\lim \limits_{k \rightarrow \infty} f(x_{best}^{(k)}) \leq f^{\ast} + \frac{5m^2G^2 t}{2}\]对于Cyclic rule,随机次梯度算法的收敛速度为\(O(m^3G^2/ \epsilon^2)\);对于Randomized rule,随机次梯度算法的收敛速度为\(O(m^2G^2/ \epsilon^2)\)。
下图给出梯度下降和随机梯度下降算法在同一数据下迭代结果: